

Next: 2.3 Proposed theories
Up: 2 Related Work
Previous: 2.1 Anatomy and physiology
Subsections
Although much is known about the anatomy of the early visual areas
such as V1, the mechanisms of visual perception are not yet fully
understood. Studies of visual illusions and aftereffects can help
provide a window into this processing, giving clues about how the
underlying systems must be operating. The tilt aftereffect is a
particularly important phenomenon to study in a model of vision, since
it is generally thought to arise in V1, the earliest cortical
processing stage. Accordingly, there have been many studies of the
TAE since the first experiments published by
Gibson and Radner in 1937.
A variety of experimental paradigms have been used to measure tilt
aftereffects in humans, but most are variations on the following
procedure (figure 2.3).
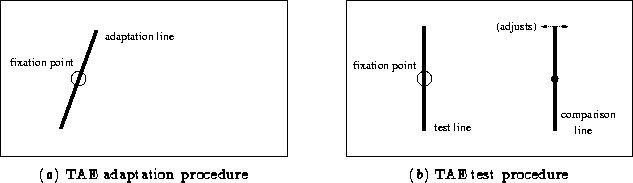
Figure 2.3:
Psychological paradigm for tilt aftereffect experiments.
The subject first adapts to a figure at a particular orientation
presented for a fixed amount of time (
a). The amount of
TAE is determined by having the subject adjust the comparison
figure to match the apparent orientation of the test figure (
b). Some studies use lines or bars, as shown here; others
show similar results for sinusoidal or square-wave gratings in
this or similar configurations.
 |
Subjects are tested in a dark room without any clues to orientation
except gravity. The subject's head is immobilized, and the subject is
directed to look at some fixation point in the visual field. Oriented
geometric figures are used in most cases, generally lines, bars, or
gratings (i.e., multiple parallel bars, as in
figure 1.1). The figures are presented in
various locations relative to the fixation point. First, a baseline
is determined by presenting a test figure at a given angle.
The perceived orientation of that figure for the subject is determined
by various methods, such as:
- Directly estimating the numerical angle.
- This is generally
considered unreliable since most subjects are poor judges of angles
other than vertical and horizontal relative to the
retina (Mansfield, 1974; Mitchell and Muir, 1976).
- Setting the figure to apparent vertical.
- This can be done
with accuracy within a degree by most unadapted subjects
(Howard and Templeton, 1966, p.179).
- Setting a comparison figure parallel to the test
figure.
- This can be done with fairly high
consistency, although it is not necessarily an accurate measure of
the actual orientation. It is particularly useful because it can
measure the effect for oblique testing angles.
After the baseline is computed, the subject views an
adaptation figure of a different orientation for a fixed amount
of time; this period is called tilt adaptation. Finally, the test
figure is presented again, and its orientation measured once more.
The difference between the final and initial readings of the perceived
orientation of the test figure is the value of the tilt aftereffect
for that particular angle separation between test and adaptation
figures
(Campbell and Maffei, 1971; Gibson and Radner, 1937; Mitchell and Muir, 1976; Muir and Over, 1970).
The TAE was first documented in detail by Gibson and Radner (1937),
who measured the angular function
(figure 2.4)
and time course
of the aftereffect.
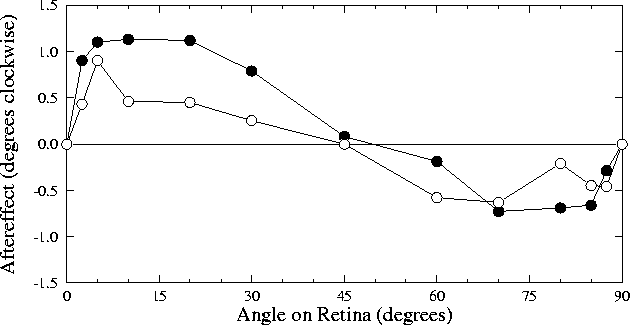
Figure 2.4:
Original study of tilt aftereffect versus
angle separation on retina.
The two lines shown indicate the tilt aftereffect for the two
different observers in
Gibson and Radner (1937). Each point
represents an average of 6 trials. Each trial consisted of a
45-second adaptation to a tilted line, then an adjustment of a
nearly vertical test line until it appeared vertical. The
difference between the perceived orientation and the actual
orientation of the test line was taken as the tilt aftereffect at
that angle. The graph shows both direct and indirect effects,
with expansion of small angles and contraction of large angles.
 |
The precise shape of the TAE versus angle curve
varies widely for different subjects and different measurement
paradigms, but generally retains the S-shape seen in
figure 2.4.
Gibson and Radner introduced terminology that describes the
aftereffect as composed of a direct effect and an
indirect effect (figure 2.5).
Figure 2.5:
Angle expansion and contraction effects.
Arrows indicate the direction of change of the perceived
orientation of that line after adaptation on the other; the
effects are equal in both directions marked
(
Mitchell and Muir, 1976). The direct effect (left) consists of a
perceived expansion of small angles, such as the one shown. The
indirect effect (center) consists of a perceived contraction of
larger angles. The maximum angle separation is 90°, since if
two endpoints are separated by larger angles than 90°, another
two form an angle smaller than 90° (right).
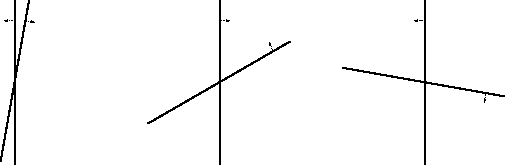 |
The direct effect consists of a perceived expansion of small angles,
i.e. the positive half of the `S' in
figure 2.5. A maximum overestimation of
a few degrees is experienced at an angular separation between 5° and 20° (Howard and Templeton, 1966, p.216). Larger angles begin to show
less of an aftereffect, eventually reaching zero somewhere between
25° and 50°
(Campbell and Maffei, 1971; Mitchell and Muir, 1976; Muir and Over, 1970). Even larger
angles (up to 90°) generally result in the indirect effect, which
consists of a smaller perceived contraction of the angle,
peaking between 60° and 85°
(Campbell and Maffei, 1971; Mitchell and Muir, 1976; Muir and Over, 1970). Note that for
overlapping lines, the largest possible separation is 90° due to
symmetry (figure 2.5).
Early studies found tilt aftereffects only for horizontal or vertical
test lines (Gibson and Radner, 1937), as did some later studies
(Campbell and Maffei, 1971). However, it has since been demonstrated that
although subjects do not spontaneously report any difference in the
perceived orientation of an oblique line (i.e., neither horizontal nor
vertical) after adaptation, when asked to set a comparison line
parallel to the test line they make systematic errors identical to
those made on vertical or horizontal test lines
(Mitchell and Muir, 1976). The variance of the settings was
significantly larger for the oblique case, which contributed to the
difficulty of establishing the effect for oblique lines. The current
consensus is that the angular separation between the test and
adaptation figures is the important parameter, not the obliqueness of
the line with respect to the horizontal or vertical axis.
The magnitude of the TAE increases logarithmically with increasing
adaptation time and decreases logarithmically with time elapsed since
the adaptation period (Gibson and Radner, 1937). However, the
magnitude of the effect saturates at approximately 4° (Campbell and Maffei, 1971; Greenlee and Magnussen, 1987; Magnussen and Johnsen, 1986; Mitchell and Muir, 1976).
The maximum indirect effect documented in central (foveal) vision is
approximately 2.5°, and reaches up to about 60% of the magnitude
of the direct effect for a given subject and paradigm
(Campbell and Maffei, 1971; Mitchell and Muir, 1976; Muir and Over, 1970). A preliminary
report indicated that only a direct effect is seen for all angles
0° to 90° when the test and adaptation figures are in
peripheral vision (Muir and Over, 1970), but this data has not yet been
replicated by other laboratories.
The TAE is localized to what appear to be a specific set of
orientation detectors. It is spatially localized on the retina
(Gibson and Radner, 1937); adaptation for a figure in one location has
no measurable effect on test figures in other locations sufficiently
distant. It is spatially selective for frequency (Ware and Mitchell, 1974);
adapting on a figure with narrow bars has no measurable effect upon a
figure with wide bars, and vice versa. Finally, it transfers
completely from one eye to the other
(Campbell and Maffei, 1971; Gibson and Radner, 1937); adapting one eye causes
equal effects upon test lines in the same location in the visual field
for either eye.



Next: 2.3 Proposed theories
Up: 2 Related Work
Previous: 2.1 Anatomy and physiology
James A. Bednar
9/19/1997