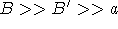 ,
the dynamics reduces to
,
the dynamics reduces to



It is straight forward to show that when the time constants 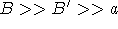 ,
the dynamics reduces to
,
the dynamics reduces to

where bold-faced quantities are matrices and vectors and <> denotes ensemble average. It is not difficult to show that this equation has a Lyapunov or ``energy'' function

which is lower bounded and satisfies

Thus the dynamics is stable. When it is stable, the output activities are decorrelated,
The above equation shows that this dynamics always leads to a stable state where the neuronal activities are decorrelated and their correlation matrix is orthonormal. Yet the connections change in an associative fashion --- equation (3) and (3) are almost Hebbian. That is why we call it associative decorrelation dynamics. From information processing point of view, a network, self-organized to satisfy equation (7), is optimized for Gaussian input ensembles and white output noises, as shown next.


