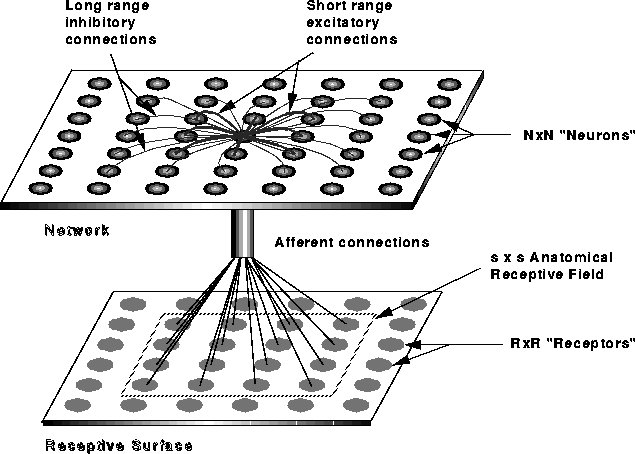
Figure 1: The RF-LISSOM
model. The lateral excitatory and lateral inhibitory
connections of a single neuron in the network are shown, together with
its afferent connections. The afferents form a local anatomical
receptive field on the retina.
The simulations are based on the RF-LISSOM
model of cortical
self-organization
[37,38,41,42].
The cortical architecture has been simplified and reduced to
the minimum necessary configuration to account for the observed
phenomena.
Because the focus is on the two-dimensional organization
of the cortex, each ``neuron'' in the model corresponds to a vertical
column of cells through the six layers of the cortex. The transformations
in the LGN were also bypassed for simplicity.
The cortical network is modeled with a sheet of interconnected neurons (figure 1). Through afferent connections, each neuron receives input from a receptive surface, or ``retina''. In addition, each neuron has reciprocal excitatory and inhibitory lateral connections with other neurons. Lateral excitatory connections are short-range, connecting only close neighbors. Lateral inhibitory connections run for long distances, and may implement close to full connectivity between neurons in the network.
Neurons receive afferent connections from broad overlapping patches on
the retina called anatomical RFs. The 
network is projected
on the retina of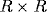 
receptors, and each neuron is assigned a
square region of receptors of side s centered on this location as its
RF. Depending on its location, the number of afferents to a neuron
could vary from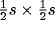 
(at the corners) to 
(at the center).
The inputs to the network consist of simple images of
multiple elongated Gaussian spots on the retinal receptors. The activity
of receptor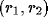 
inside a spot is given by
where 
and 
specify the length along the
major and minor axes of the Gaussian, 
specifies its orientation
(chosen randomly from the uniform distribution in the
range 
), and (
,
): 
specifies its center.
The elongated Gaussian spots approximate natural visual stimuli after
the edge detection and enhancement mechanisms in the retina.
Both afferent and lateral connections have positive synaptic weights.
The weights are initially set to random values, and organized through an
unsupervised learning process. At each training step, neurons start out
with zero activity. An elongated pattern is introduced on the retina,
and the activation propagates through the afferent connections to the
cortical network. The initial response
of neuron 
is calculated as a weighted sum of the retinal activations:
where 
is the activation of a retinal receptor
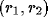within the receptive field of the neuron, 
is
the corresponding afferent weight, and 
is a piecewise linear
approximation of the familiar sigmoid activation function.
The response evolves over time through lateral interaction.
At each time step, each cortical
neuron combines the above afferent activation 
with its
lateral excitation and inhibition:
where 
is the excitatory lateral connection weight on the
connection from neuron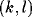 
to neuron 
, 
is the
inhibitory connection weight, and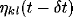 
is the
activity of neuron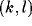 
during the previous time step. In other
words, the retinal activity stays constant while the cortical response
settles.
The scaling factors 
and 
determine the strength of the lateral excitatory and inhibitory
interactions.
The activity pattern starts out diffuse and
spread over a substantial part
of the map, and converges iteratively into stable focused patches of
activity, or activity bubbles.
After the activity has settled, typically in a few iterations of equation 3, the connection weights of each neuron are modified. Both afferent and lateral weights adapt according to the same mechanism: the Hebb rule, normalized so that the sum of the weights is constant:
where 
stands for the activity of the neuron 
in the
settled activity bubble, 
is the afferent or the lateral
connection weight (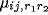
, 
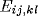or 
),
is the learning rate for each type of connection (
for afferent weights, 
for excitatory, and 
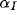for
inhibitory) and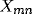 
is the presynaptic activity (
for afferent, 
for lateral). Afferent inputs, lateral excitatory
inputs, and lateral inhibitory inputs are normalized separately.
Both inhibitory and excitatory lateral connections follow the same Hebbian learning process and strengthen by correlated activity. At long distances, very few neurons have correlated activity and therefore most long-range connections eventually become weak. The weak connections are eliminated periodically, and through the weight normalization, inhibition concentrates in a closer neighborhood of each neuron. The radius of the lateral excitatory interactions starts out large, but as self-organization progresses, it is decreased until it covers only the nearest neighbors. Such a decrease is necessary for global topographic order to develop and for the receptive fields to become well-tuned at the same time (for theoretical motivation for this process, see [26,27,28,33,42]; for neurobiological evidence, see [9,20].) Together the pruning of lateral connections and decreasing excitation range produce activity bubbles that are gradually more focused and local. As a result, weights change in smaller neighborhoods, and receptive fields become better tuned to local areas of the retina.
