Having discussed how cortical structures could develop by self-organization, and how they may be maintained in a dynamic equilibrium in the adult, let us now turn to the functional role of these self-organized structures in visual processing. Field and Barlow [3,11,12] suggested that the RFs in the primary visual cortex act as filters that form a sparse coding of the visual input. This is a hypothesis that is difficult to study experimentally, but a computational model such as the one presented in this paper is ideal for testing it. Sparse codes minimize the number of active neurons in the cortex, and are well suited for the detection of suspicious coincidences, associative memory and feature grouping [2,3,12]. It will be shown below that (1) the network forms a sparse coding of the input, (2) the coding reduces redundancies, and (3) self-organized lateral connections are crucial to get these effects.
By Hebbian self-organization, the lateral connections in the model learn correlations between the feature-selective cells. The stronger the correlation between two cells, the larger the connection strength between them. Because the long-range connections are inhibitory, strongly correlated regions of the network inhibit each other. At the same time, the short-range lateral excitation locally amplifies the responses of active neurons. Together, the recurrent excitation and inhibition focuses the activity to the neurons best tuned to the features of the input stimulus, thereby producing a sparse coding of the input. Sparseness can be measured by the kurtosis (i.e. peakedness) of the network response [12]. A small number of strongly-responding neurons, that is, a sparse coding, will result in high kurtosis. Figure 6 shows the kurtosis before and after lateral interactions. The main result is that with self-organized lateral interactions, kurtosis is substantially higher, demonstrating that lateral interactions recode the afferent activity into the strong responses of a few neurons.
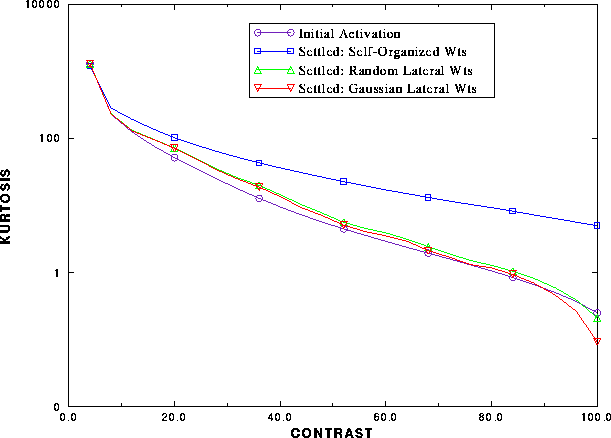
Figure 6: Sparse coding in the
self-organized network.
The kurtosis of the network response is plotted (1) before lateral
interaction, and after lateral interaction with (2) self-organized
lateral weights, (3) fixed random lateral weights and (4) fixed Gaussian
lateral weights. As the contrast in the input increases (measure by the
intensity of the light spots, in percentage), the kurtosis
(and hence the sparseness) of both the initial activity and the settled
activity with predetermined weights decrease together. However, when the
lateral connections are self-organized, the curve diverges, and the
kurtosis of the activity remains high even at full contrast, indicating
that the self-organized lateral connections perform redundancy reduction
on the response.
An efficient scheme of sparse encoding would reduce the redundancies in the activation pattern as much as possible. To demonstrate that the network performs such efficient redundancy reduction, the kurtosis was calculated and plotted for various levels of input contrast, as in figure 6. A constant pattern of several elongated Gaussian light spots was presented to the retina, and the height of the Gaussians was systematically increased. As the light spots become more intense, increasing the contrast in the input, there is more total input activation to the network. The number of neurons activated by the constant input pattern increases, resulting in larger amounts of redundant activity. If the lateral connections perform redundancy reduction, then at higher contrasts one would expect more redundancy reduction than at lower contrasts. As a result, the kurtosis graphs of the initial activation and the settled activation should diverge. This is indeed the case, as can be seen in figure 6.
It also turns out that self-organization is crucial to reduce the redundancies efficiently. To show this, the kurtosis changes were compared in four cases: (1) the initial response before the lateral interactions, (2) the response after lateral interactions when the lateral connections were self-organized, (3) the same when the lateral connections were fixed to random weight values, and (4) when they were fixed to a Gaussian profile (as assumed in some of the early self-organizing models). As figure 6 indicates, the kurtosis in the first case (initial response) falls off sharply with contrast, as would be expected from a linear (or semi-linear) system. The result is approximately the same when the lateral connections have random or Gaussian weights. However, when the lateral connectivity is self-organized, the kurtosis is much higher, and increasing amount of redundancy reduction is performed at high contrasts.
Figure 7: Invariance of orientation selectivity with contrast. At each contrast, the response
after lateral interactions of a typical neuron to stimuli
at different orientations are plotted.
As contrast is increased, the peak response increases,
but beyond about 20% contrast, the bandwidth of orientations to
which the cell responds remains approximately constant.
The sparse coding produced by lateral interactions also manifests itself in the orientation selectivity of neurons. Figure 7 illustrates the orientation tuning of a cell in the self-organized network measured from the settled response at different contrasts. Even as contrast increases, the orientation selectivity of the cell remains sharp. Because of lateral interactions, the cells in the network do not act as linear filters, but more like nonlinear feature detectors that are sharply tuned to limited regions of the input space. Similar observations have recently been made in the visual cortex [36,43].