


Next: Postscript
Up: Synchronous Oscillations Based on
Previous: Why Local Connections?
This chapter elucidates a mechanism for reaching emergent synchrony in
a network of oscillators by only local connections. There are two main
parts to this mechanism: (1) a more detailed, possibly more plausible,
oscillator model is used; (2) The dynamic normalization principle (Equation 2)
to ensure the equal weight condition for the communication among the
oscillators. Dynamic normalization provides a quantitative procedure
for the idea of dynamic links, which has been argued to be neurally
plausible (see von der Malsburg
[62], Crick
[12]). Based on this
mechanism, the simulation results of synchronous oscillations in the
visual cortex well match the corresponding experimental results. We
note that the models of Sporns et al.
[56], König and Schillen
[34],
Wilson and Bower
[73], and Chawanya et al.
[10] can also simulate
the experimental results based on local coupling. Our model differs
from Sporns et al.
[56,57], Wilson and Bower
[73], and
Chawanya et al.
[10] in that we provide a general mechanism of
reaching global synchronization based on local connections. As stated
in the introduction, the model of König and Schillen
[34] relies on
specific delay relations to obtain phase synchronization, while ours does not.
Perhaps more importantly, we consider synchronous oscillations based on
local connections represent a significant step towards solving
engineering problems of scene segmentation and figure/ground segregation.
Although a number of attempts have been made to use neural oscillations
for solving the problem of sensory segmentation
[4,43,55,64,63], the progress
in general is very limited and does not meet people's expectations
(see
[62]). We think that the lack of a local
mechanism has been one of the major difficulties to be overcome before
neural oscillations can play a significant role in machine pattern analysis.
The network architecture illustrated in the Why Local ... lays a ground for a novel
approach to neural scene segmentation. The permanent connection pattern
(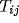 's of (4)) of the network defines the innate architecture, which is
simple and sufficiently general. Dynamic connections (
's of (4)) of the network defines the innate architecture, which is
simple and sufficiently general. Dynamic connections ( 's) are
formed on the basis of the permanent connections and current input
patterns. Synchronous oscillations make the result of segmentation
readily utilizable - a simple threshold function would do the job.
The neighborhood connectivity pattern preserves the geometrical structures
of the objects. If one allows lateral connections beyond nearest
neighbors or adds more layered structures of the network, both the
capability and the flexibility of scene segmentation should be markedly
enhanced. These features are very attractive compared to the traditional
approach of image segmentation, where edge detection is followed by
contour detection and then a process of labeling different regions
based on closed contours, among other heuristics
[17,25,49]. The approach offered
here directly operates on objects, without the detour of detecting contours
from regions and then forming regions based on contours, often an
ambiguous process.
's) are
formed on the basis of the permanent connections and current input
patterns. Synchronous oscillations make the result of segmentation
readily utilizable - a simple threshold function would do the job.
The neighborhood connectivity pattern preserves the geometrical structures
of the objects. If one allows lateral connections beyond nearest
neighbors or adds more layered structures of the network, both the
capability and the flexibility of scene segmentation should be markedly
enhanced. These features are very attractive compared to the traditional
approach of image segmentation, where edge detection is followed by
contour detection and then a process of labeling different regions
based on closed contours, among other heuristics
[17,25,49]. The approach offered
here directly operates on objects, without the detour of detecting contours
from regions and then forming regions based on contours, often an
ambiguous process.
Of course, scene segmentation involves many issues other than the
separation of connected regions, such as segmentation based on depth
(see Murata and Shimizu
[43], for an interesting handling by synchronous
oscillations), occlusion, intersection, and so on. Although its eventual
applicability to segmentation must be judged by future research, the
basic principle of the approach introduced here, namely, the emergent
properties from local communications, will be, we believe, a fundamental
part of a successful system of real-time scene understanding.



Next: Postscript
Up: Synchronous Oscillations Based on
Previous: Why Local Connections?
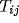 's of (4)) of the network defines the innate architecture, which is
simple and sufficiently general. Dynamic connections (
's of (4)) of the network defines the innate architecture, which is
simple and sufficiently general. Dynamic connections ( 's) are
formed on the basis of the permanent connections and current input
patterns. Synchronous oscillations make the result of segmentation
readily utilizable - a simple threshold function would do the job.
The neighborhood connectivity pattern preserves the geometrical structures
of the objects. If one allows lateral connections beyond nearest
neighbors or adds more layered structures of the network, both the
capability and the flexibility of scene segmentation should be markedly
enhanced. These features are very attractive compared to the traditional
approach of image segmentation, where edge detection is followed by
contour detection and then a process of labeling different regions
based on closed contours, among other heuristics
[17,25,49]. The approach offered
here directly operates on objects, without the detour of detecting contours
from regions and then forming regions based on contours, often an
ambiguous process.
's) are
formed on the basis of the permanent connections and current input
patterns. Synchronous oscillations make the result of segmentation
readily utilizable - a simple threshold function would do the job.
The neighborhood connectivity pattern preserves the geometrical structures
of the objects. If one allows lateral connections beyond nearest
neighbors or adds more layered structures of the network, both the
capability and the flexibility of scene segmentation should be markedly
enhanced. These features are very attractive compared to the traditional
approach of image segmentation, where edge detection is followed by
contour detection and then a process of labeling different regions
based on closed contours, among other heuristics
[17,25,49]. The approach offered
here directly operates on objects, without the detour of detecting contours
from regions and then forming regions based on contours, often an
ambiguous process.