Forming

 

For this operation to be well-defined, we require matrices A , B , and C to have dimensions , , and , respectively.

We start my noting that if we partition A and B by columns and rows, respectively,

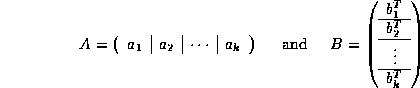
then

Thus, a matrix-matrix multiply can be written as a sequence of rank-one updates.

Basic Parallel Algorithm:

We can implement the above sequence of rank-1 updates by using views, splitting off one column and row at a time: Let A and B be partitioned like

where and equal the first column of A and first row of B . Then

So the update of C can be viewed as an initial scaling of C , followed by a rank-1 update with the first column and row of A and B, respectively. After this, the operation can be performed, using the same approach, recursively.

This leads to the following algorithm:

• Scale
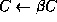
• Let and
• Do until done
  • If and are empty, the loop is done.
  • Partition

    

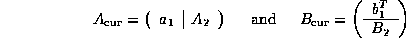
  • Update
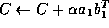
  • Let and

Here the `` '' symbol is used to indicate assignment, while ``='' indicates a reference or partitioning. The resulting PLAPACK code is given in Figure . When comparing the main loop in this code to that given for rank-1 update in Figure , notice that we have merely added a loop that creates appropriate views into matrices A and B .

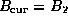
PLACE BEGIN HR HERE

PLACE END HR HERE

Blocked Algorithm:

In order to get better performance, it is advantageous to set up the algorithm to perform a sequence of rank-k updates instead: Let A and B be partitioned like

where and are is a and matrices, respectively. Then

This leads to the following algorithm:

• Scale
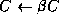
• Let and
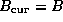
• Do until done
  • Determine width s of split. If and are empty, the loop is done.
  • Partition

    

    and

    

    where and are is a and matrices, respectively.

  • Update
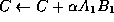
  • Let and

Again, the `` '' symbol is used to indicate assignment, while ``='' indicates a reference or partitioning. This blocked code is given in Fig. . We will often refer to this approach to parallel matrix-matrix multiplication as a     panel-panel variant, to indicate that the basic operation uses panels of each of the matrices (rank-k update).

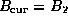
PLACE BEGIN HR HERE

PLACE END HR HERE

Pipelined Algorithm:

When k is large, the above algorithm can be improved by introducing pipelining. This can be accomplished by setting the natural flow of computation to be to the right for communication within rows and down for communication within columns. We will assume this has been done before entering the matrix multiplication routine, using the calls

PLA_Temp_set_comm_dir( template, PLA_TEMP_ROW, PLA_DIR_RIGHT );
PLA_Temp_set_comm_dir( template, PLA_TEMP_COL, PLA_DIR_DOWN );

For details on the benefits of pipelining, see [, ].