In Section 1.2,
we gave the following description for the Cholesky factorization
of 
matrix A:
where 
and 
are scalars and 
and 
are vectors of length n-1 .
The 
indicates the symmetric part of A .
Now,
This in turn yields the equations
We conclude that the following steps will implement the Cholesky factorization, overwriting the lower triangular portion of A with L :
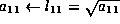
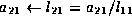
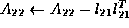
- compute the Cholesky factorization of updated
recursively, yielding
.
Given the PLAPACK level-1 and level-2 BLAS operations described in
previous chapters, a complete implementation
is given in
Figure 8.1.
In this implementation, the ``current'' matrix A is
referenced by acur. The routine Take_sqrt
overwrites the view of 
sub-matrix 
by
its square-root. The comments to the right of the algorithm
give essentially the description of the algorithm as
presented in the text. Notice that indeed the code is
line-for-line a translation of this algorithm.