Let us consider the simple example of implementation
of the
Cholesky factorization, which we will revisit
in Chapter ![]() .
Given a symmetric
.
Given a symmetric ![]() positive definite matrix A , the Cholesky
factorization of A is given by
positive definite matrix A , the Cholesky
factorization of A is given by
![]()
where L is lower triangular.
The algorithm for implementing this operation can be described by partitioning (blocking) the matrices
![]()
where ![]() and
and ![]() are scalars, and
are scalars, and ![]() and
and ![]() are vectors of length n-1 .
The
are vectors of length n-1 .
The ![]() indicates the symmetric part of A .
Now,
indicates the symmetric part of A .
Now,
![]()
This in turn yields the equations

We now conclude that the following steps will implement the Cholesky factorization, overwriting the lower triangular portion of A with L :
We make a few observations:
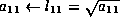
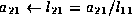
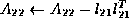
- compute the Cholesky factorization of updated
recursively, yielding
.
The primary opportunity for parallelism is in the symmetric rank-1 update:
- The algorithm does not index individual elements of the original matrix explicitly. Notice it references different parts of the current matrix, not the original matrix.
- The blocks are simply references into the original matrix.
- There is an inherent use of recursion.
Using the PLAPACK infrastructure, parallel code for the above algorithm is given by
PLA_Obj_view_all( a, &acur );
while ( TRUE ){
PLA_Obj_global_length( acur, &size );
if ( 0 == size ) break;
PLA_Obj_split_4( acur, 1, 1, &a11, &a12,
&a21, &acur );
Take_sqrt( a11 );
PLA_Inv_scal( a11, a21 );
PLA_Syr( PLA_LOW_TRIAN, min_one, a21, acur );
}
Previewing the rest of the book,
all information that describes A , its data, and how it
is distributed to processors (nodes) is encoded in an
object (data structure) referenced by a.
The PLA_Obj_view_all creates a second reference,
acur, into the same data.
The PLA_Obj_global_length call extracts the current
size of the matrix that acur references.
If this is zero, the recursion has completed.
The call to PLA_Obj_split_4 partitions the
matrix, creating new references for the four quadrants.
Element In order to understand how parallelism is achieved in the above calls, we must first examine how PLAPACK distributes vectors and matrices, in Section 1.3. After this, we show how operations like the symmetric rank-1 update can be naturally parallelized, in Sections 1.5 and 1.6.