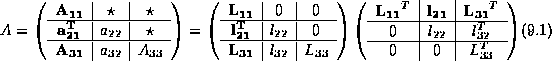
Consider the partitioning
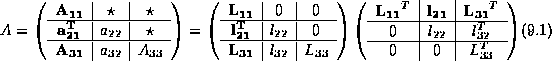
The blockings of matrices A and L are identical.
Blocks 
and 
are scalars, 
and
are row vectors,
and 
and 
are column vectors. Sub-matrices
, 
, 
, and
are square matrices.
The assumption is that bold-face parts of the lower triangular
matrix have already been computed, and have overwritten the
corresponding parts of A . The rest of the matrix has not
been updated at all, and the object of the next step is
to compute the next parts of the lower triangular matrix,
and , overwriting the corresponding parts of
A .
From the above equation, we derive
Thus if 
and are to be updated
by and 
, the following step will suffice:
The algorithm of left looking version of Cholesky factorization can be given as follows using the above equations
The PLAPACK implementation using global level-2 BLAS is given in Figure 8.3. In this code, at the top of the loop, a_1 references the matrix
- Update the current panel according to Equation
.
- Continue recursively by repartitioning the matrix.
and a_cur the matrix
