2.3.1 Linear algebra object creation

  The     linear algebra object creation routines create the object that stores the information required to describe the object. This includes parameters like the data type, the template with which the object is aligned, the alignment itself, as well as the global dimensions of the object. We will describe the calls required to create the different linear objects next.

The     data type of an object can equal any   MPI data type, but will typically equal one of MPI_INT, MPI_FLOAT, MPI_DOUBLE, MPI_COMPLEX and MPI_DOUBLE_COMPLEX. Notice that neither MPI_COMPLEX nor MPI_DOUBLE_COMPLEX are standard MPI data types for the C programming language. However, they are frequently used in linear algebra packages. On architectures where MPI does not define these, the PLAPACK infrastructure itself does upon initialization of the environment, to reflect the FORTRAN language conventions for storing complex and double precision complex numbers.

Vectors and multivectors:

            To create a vector, we indicate the   data type, the   global length, the template to be used, and the   alignment of the vector to the template (see Figure 2.1). Often, it will be convenient to work with a group of vectors simultaneously, which we call a multivector. All vectors in a multivector are of equal length and are identically aligned. Thus, one can think of a multivector as a matrix with a few columns, where all columns are identically distributed, like vectors. A multivector object is created by indicating the   data type,   global length (length of each vector in the multivector),   global width   (number of vectors comprising the multivector), template, and the   alignment to the template. This alignment holds for all vectors in the multivector, as illustrated in Figure 2.1.

Since indexing in the template can start with either zero or one, the constant

PLA_ALIGN_FIRST can be used to indicate the first element in the template.

Matrices:

      Matrices require a   data type,   global length,   global width, template, and both a   row and column alignment. The call becomes

Again, PLA_ALIGN_FIRST can be used to indicate alignment with the first row and/or column of the template matrix.

Multiscalar:

      We have the notion of a multiscalar, which is a linear algebra object that exists as a unit entirely within one node (i.e., it is NOT distributed). This multiscalar may or may not be duplicated within one row, one columns, or all nodes, as indicated in the creating call. In general, the multiscalar is an non-distributed matrix, with row and column dimension.

The owner_row and owner_col parameters can take on any integers which equal the row and column indices, respectively, of a node in the node mesh. In addition, owner_row can take on the value PLA_ALL_ROWS, which indicates that all nodes in the column indicated by owner_col own a copy of the multiscalar. Similarly, parameter owner_col can take on the value PLA_ALL_COLS, which indicates that all nodes in the row indicated by owner_row own a copy of the multiscalar. All nodes own a copy if owner_row = PLA_ALL_ROWS and owner_col = PLA_ALL_COLS.

Projected vectors and multivectors:

           As part of a parallel implementation of an algorithm, we may need a row vector or column vector to exist within one or all row(s) or column(s) of nodes. To create such an object, one uses the     rojected vector create routine. Together with the calling sequence for creating a projected vector, we also give the calling sequence for creating a    projected multivector, which is the natural extension of the concept to multivectors:

Here project_onto equal to PLA_PROJ_ONTO_ROW or PLA_PROJ_ONTO_COL indicates whether the (multi)vector is created by projecting against a row or column of the mesh of nodes, respectively. Parameter owner indicates which row or column owns the projected (multi)vector. If owner equals PLA_ALL_ROWS or PLA_ALL_COLS, all rows or all columns of nodes own a copy of the object, respectively. The global_align parameter indicates the alignment to the matrix template after projection. If project_onto equals PLA_PROJ_ONTO_ROW, the value of the global_align parameter can also be interpreted as the global column alignment with respect to the matrix template of the projected (multi)vector. Similarly, if project_onto equals PLA_PROJ_ONTO_COL, the value of the global_align parameter can also be interpreted as the global row alignment with respect to the matrix template of the projected (multi)vector. The constant PLA_ALIGN_FIRST can be used to indicate alignment with the first row or column of the template matrix.

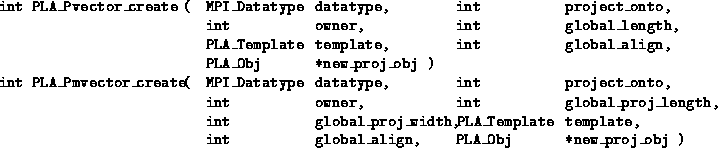
When creating a projected (multi)vector, global_proj_length and global_proj_width warrant special attention. Notice that a projected (multi)vector is much like a matrix of similar length and width. However, depending on whether the (multi)vector is projected against a column or row, the roles of the global length and width of the multivector may be reversed. To avoid confusion, we dictate that the global length and width given for a projected multivector reflect the global length and width of the multivector after projection.

Note: All nodes that should be aware of the existence of an object need to make identical calls to the creation routine. Thus, it is possible that the call is made by one node, by one column of nodes, by one row of nodes, or by all nodes. It is not necessarily the case that only a node that owns actually data that is encoded in the object must make the call. For example, if one wishes to copy a sub-matrix from a global matrix to a multiscalar owned by one node, all nodes must be aware of the existence of the multiscalar, and thus all nodes must have created the multiscalar. Enforcing consistency is the responsibility of the calling routine, not the creation routine.