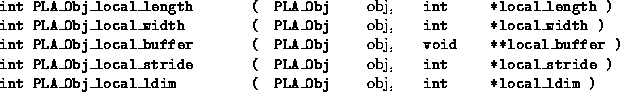As for the template object, we do not permit the data structure that encodes the linear algebra object to be accessed directly. Instead, we provide inquiry routines, which can be used to query information about the linear algebra object. The general rule is that all linear algebra object inquiry routines start with PLA_Obj_ followed by the name of the field required.
This category of inquiry routines provides information that is often useful when dealing with a given object at the global level (without specifically addressing local information) as well as when operations specific to the local portion of an object are to be performed. It includes calls to inquire the object type, the data type, and the template used to create the object.
![]()
![]()
![]()
![]()
The return value equals PLA_UNDEFINED if the object type is not recognized.
The object data type is extracted by calling
![]()
![]()
![]()
![]()
The template used to create the object is extracted by calling
![]()
![]()
![]()
Ideally, code written using PLAPACK deals only with global information about the object, including the global dimensions, the alignment of the object to the template, the dimension of the processing mesh onto which a (multi)vector is projected, and/or the row or column of the node mesh that owns a projected (multi)vector. The following call returns these values for a given object:

![]()

For projected (multi)vectors, parameter project_onto returns one of values PLA_PROJ_ONTO_ROW or PLA_PROJ_ONTO_COL. Parameters owner_row and owner_col return the index of the row or column of nodes that owns the projected (multi)vector or multiscalar. If the projected (multi)vector or multiscalar is duplicated these may equal PLA_ALL_ROWS and/or PLA_ALL_COLS. Notice that for some of the objects some of the parameters have no meaning, in which case the value PLA_UNDEFINED is returned. The alignment parameters indicate alignment with respect to the template.
As for the template inquiry routines, we also provide calls for extracting specific parameters:

Here we have added the call PLA_Obj_global_size to return the length of a (duplicated) (projected) (multivector) when viewed as a vector, to overcome the already mentioned confusion of what the length of such an object is. Also, the call PLA_Obj_global_numvecs can be used to extract the number of vectors in a (duplicated) (projected) multivector.
Some routines need to gain access to information concerning the part of a linear algebra object assigned to a node. For this, we provide calls that return this information for the part of the object assigned to the node that makes the call.
Before discussing the local information calls, we must discuss
how PLAPACK locally stores the data associated with the different
linear algebra objects.
Let us consider a vector x distributed to a ![]() mesh
of nodes. For simplicity, we will assume that the vector is
aligned to the first entry of the template vector, which is
partitioned using a distribution blocking size
mesh
of nodes. For simplicity, we will assume that the vector is
aligned to the first entry of the template vector, which is
partitioned using a distribution blocking size ![]() .
Thus
.
Thus

where ![]() is of length
is of length ![]() (except perhaps the last sub-vector).
Node (i,j) will own the sub-vectors
(except perhaps the last sub-vector).
Node (i,j) will own the sub-vectors

This vector is locally stored in memory so that the order of
the elements is preserved (i.e., elements of ![]() will precede those of
will precede those of ![]() ).
The
stride in memory between elements will be internally determined, and
can be inquired by one of the subsequently described calls.
).
The
stride in memory between elements will be internally determined, and
can be inquired by one of the subsequently described calls.
Next, let us consider a matrix A distributed to the same mesh. For simplicity, we assume that A is aligned with the upper-left element of the template matrix induced by the above mentioned template vector. Then,
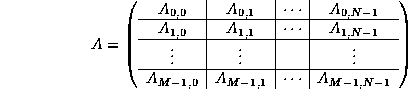
and the following sub-matrix is assigned to node (i,j) :

It is this matrix ![]() that is stored in a local
two-dimensional array, using FORTRAN style
column-major
order storage, with a
leading dimension determined internal
to PLAPACK.
that is stored in a local
two-dimensional array, using FORTRAN style
column-major
order storage, with a
leading dimension determined internal
to PLAPACK.
Finally, let us discuss the storage of a projected multivector. Notice that if the vector x discussed above is spread within a column of nodes, or gathered to the i th node in each column, the following sub-vectors will be collected on node (i,j) :
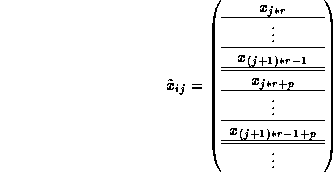
Notice that the sub-vectors from within a column of nodes are interleaved so that the indices of sub-vectors are strictly increasing (the order in the global vector is maintained). It is this vector that is then stored in a local linear array, with a stride determined internal to PLAPACK.
The primary call to extract the local information is given by
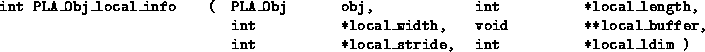
![]()

Notice that it is entirely possible that the part of a linear algebra object that a given node owns is empty. In this case, local_length and/or local_width will equal zero, and the local_buffer pointer may not have a meaningful value. In particular, local_buffer may equal NULL in this situation.
- Vector: The local length of the (projected) vector is returned in local_length and local_width equals one. The stride to get from one element to the next is returned in local_stride. The last parameter has no meaning and returns PLA_UNDEFINED.
- Matrix: The local length and local width are returned in local_length and local_width. The leading dimension of the local buffer that holds the local matrix is returned in local_ldim. Parameter local_stride returns PLA_UNDEFINED.
- Multivector: The local length and width are returned in local_length and local_width. If the multivector is unprojected, or projected against a column, then the local width will always equal the global width. If the multivector is projected against a row, the local length will always equal the global length. The leading dimension of the local buffer that holds the local part of the multivector, which is locally just a matrix, is returned in local_ldim. Parameter local_stride returns PLA_UNDEFINED.
- Multiscalar: The local length and width are returned in local_length and local_width. On the nodes that own the multiscalar, as indicated by the owner_row and/or owner_col parameters when the multiscalar is created, the local and global length are identical, as are the local and global width. The leading dimension of the local buffer that holds the local part of the multiscalar, which is locally just a matrix, is returned in local_ldim. Parameter local_stride returns PLA_UNDEFINED.
As for the template and object global inquiry routines, we also provide calls for extracting specific parameters: