We now give a brief overview of a building-block approach to implementing the copy. The goal is to show that while all message passing complexity in our library has been pushed onto the copy and reduce routines, the complexity of the implementation is manageable, and efficiency can be attained if the implementation of the MPI collective communication library on a given architecture is reasonable.
We will start by describing how a multivector
(unprojected, projected, and/or duplicated) can be copied
to any other multivector using a few simple operations.
By taking the multivector to consist of only one vector,
we also capture the case of copying a
(duplicated) (projected) vector to a (duplicated) (projected) vector.
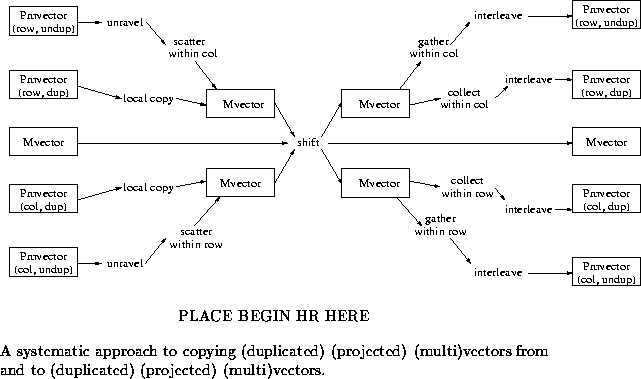
This process is illustrated in Figure 
.
Let us assume that two given multivector objects have the same global dimensions, allowing a copy of the contents of one to the other to proceed. There are two cases to consider:
- Alignment matches: If the global alignment of the multivectors agrees, merely a local copy of the contents is required.
- Alignment does not match: In this case, the contents must be shifted, aligning the contents to the output alignment. Given the current restrictions on distribution templates, this requires all nodes to send data to at most two other nodes.
Recall that the terminology ``projected'' multivector comes from the fact that it can be viewed as a multivector that has been projected against one of the mesh dimensions, row or column, requiring a gather within individual columns or rows, respectively. Again, there are two cases to consider:
- Alignment matches: If the global alignment of the target projected multivector matches that of the source multivectors, logically a gather within the appropriate mesh dimension suffices. Notice however that due to the fact that multivectors are wrapped onto the mesh of nodes, an interleaving of elements must occur when projecting (Figure
- Alignment does not match: Rather than trying to perform this operation in a single step, we propose the following: Create a multivector that is aligned with the target projected multivector. Copy from the source multivector to this intermediate result, and use the case above to copy from the aligned multivector to the projected multivector.
Naturally, this operation reverses the steps required for copying a multivector to an unduplicated projected multivector, requiring an unravel (inverse of the interleave) followed by a call to MPI_Scatter (inverse of the gather).
One can attain a copy of a multivector to duplicated projected multivector by simply replacing the gather in the copy from multivector to unduplicated projected multivector by a collect (MPI_Allgather). Again, alignment, if necessary, can be achieved through an intermediate multivector.
Again, we can use intermediate distributions to copy any unduplicated projected multivector to a duplicated projected multivector: create an intermediate multivector, copy from unduplicated multivector to the intermediate object, followed by a copy from the intermediate object to the target. Notice this involves a packing (unraveling), a scatter within one dimension of the mesh, a shift (if necessary), a collect within one (possibly the same) dimension of the mesh, and an unpacking (interleaving).
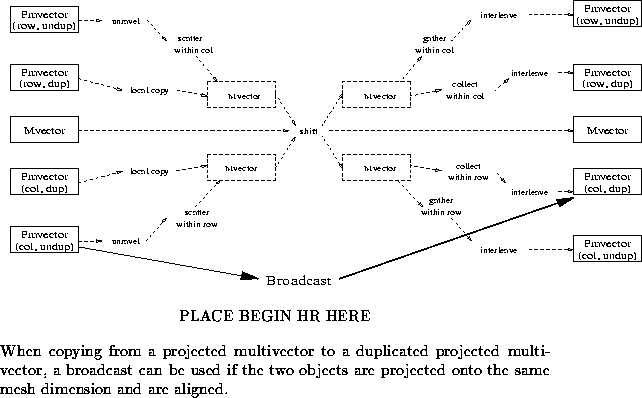
If the source and target projected multivectors
are both projected against the same mesh dimension, and
are aligned, the pack, scatter, collect, and unpack can all
be combined into one operation: a broadcast of the
the contents within the appropriate mesh dimension.
While the scatter and collect together provide for an efficient
broadcast for large volumes of data, viewing it as just
a broadcast allows for the appropriate implementation of that
operation to be used. Moreover, on many architectures, the
pack and unpack are the primary expense in these communications.
This shortcut is illustrated in Figure .
Figure captures all possible operations
required to copy one multivector to another. This figure does
not include possible shortcuts.
PLACE BEGIN HR HERE
PLACE END HR HERE
PLACE BEGIN HR HERE
PLACE END HR HERE
Notice that copying a matrix to another matrix or a (projected) multivector can be achieved by viewing the rows or columns of the matrix as a collection of projected multivectors, which can be copied individually.
We don't expect that copies involving multiscalars will contribute significantly to the overall expense of most algorithms implemented using PLAPACK. We thus don't cover the details of this subject in this book.