ALAFF Welcome

Skip to main content

\( \usepackage{array} \setlength{\oddsidemargin}{-0.0in} \setlength{\evensidemargin}{-0.0in} \setlength{\textheight}{8.75in} \setlength{\textwidth}{6.5in} \setlength{\topmargin}{-0.25in} \newcommand{\R}{\mathbb R} \newcommand{\Rm}{\mathbb R^m} \newcommand{\Rn}{\mathbb R^n} \newcommand{\Rnxn}{\mathbb R^{n \times n}} \newcommand{\Rmxn}{\mathbb R^{m \times n}} \newcommand{\Rmxm}{\mathbb R^{m \times m}} \newcommand{\Rmxk}{\mathbb R^{m \times k}} \newcommand{\Rkxn}{\mathbb R^{k \times n}} \newcommand{\C}{\mathbb C} \newcommand{\Cm}{\mathbb C^m} \newcommand{\Cmxm}{\mathbb C^{m \times m}} \newcommand{\Cnxn}{\mathbb C^{n \times n}} \newcommand{\Cmxn}{\mathbb C^{m \times n}} \newcommand{\Ckxk}{\mathbb C^{k \times k}} \newcommand{\Cn}{\mathbb C^n} \newcommand{\Ck}{\mathbb C^k} \newcommand{\Null}{{\cal N}} \newcommand{\Col}{{\cal C}} \newcommand{\Rowspace}{{\cal R}} \newcommand{\Span}{{\rm {Span}}} \newcommand{\rank}{{\rm rank}} \newcommand{\triu}{{\rm triu}} \newcommand{\tril}{{\rm tril}} \newcommand{\sign}{{\rm sign}} \newcommand{\FlaTwoByTwo}[4]{ \left( \begin{array}{c | c} #1 \amp #2 \\ \hline #3 \amp #4 \end{array} \right) } \newcommand{\FlaTwoByTwoSingleLine}[4]{ \left( \begin{array}{c c} #1 \amp #2 \\ #3 \amp #4 \end{array} \right) } \newcommand{\FlaTwoByTwoSingleLineNoPar}[4]{ \begin{array}{c c} #1 \amp #2 \\ #3 \amp #4 \end{array} } \newcommand{\FlaOneByTwo}[2]{ \left( \begin{array}{c | c} #1 \amp #2 \end{array} \right) } \newcommand{\FlaOneByTwoSingleLine}[2]{ \left( \begin{array}{c c} #1 \amp #2 \end{array} \right) } \newcommand{\FlaTwoByOne}[2]{ \left( \begin{array}{c} #1 \\ \hline #2 \end{array} \right) } \newcommand{\FlaTwoByOneSingleLine}[2]{ \left( \begin{array}{c} #1 \\ #2 \end{array} \right) } \newcommand{\FlaThreeByOneB}[3]{ \left( \begin{array}{c} #1 \\ \hline #2 \\ #3 \end{array} \right) } \newcommand{\FlaThreeByOneT}[3]{ \left( \begin{array}{c} #1 \\ #2 \\ \hline #3 \end{array} \right) } \newcommand{\FlaOneByThreeR}[3]{ \left( \begin{array}{c | c c} #1 \amp #2 \amp #3 \end{array} \right) } \newcommand{\FlaOneByThreeL}[3]{ \left( \begin{array}{c c | c} #1 \amp #2 \amp #3 \end{array} \right) } \newcommand{\FlaThreeByThreeBR}[9]{ \left( \begin{array}{c | c c} #1 \amp #2 \amp #3 \\ \hline #4 \amp #5 \amp #6 \\ #7 \amp #8 \amp #9 \end{array} \right) } \newcommand{\FlaThreeByThreeTL}[9]{ \left( \begin{array}{c c | c} #1 \amp #2 \amp #3 \\ #4 \amp #5 \amp #6 \\ \hline #7 \amp #8 \amp #9 \end{array} \right) } \newcommand{\diag}[1]{{\rm diag}( #1 )} \newcommand{\URt}{{\sc HQR}} \newcommand{\FlaAlgorithm}{ \begin{array}{|l|} \hline \routinename \\ \hline \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\FlaAlgorithmWithInit}{ \begin{array}{|l|} \hline \routinename \\ \hline \initialize \\ \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\FlaBlkAlgorithm}{ \begin{array}{|l|} \hline \routinename \\ \hline \partitionings \\ ~~~ \begin{array}{l} \partitionsizes \end{array} \\ {\bf \color{blue} {while}~} \guard \\ ~~~ {\bf choose~block~size~} \blocksize \\ ~~~ \begin{array}{l} \repartitionings \end{array} \\ ~~~ ~~~ \repartitionsizes \\ ~~~ \color{red} { \begin{array}{l} \hline \color{black} {\update} \\ \hline \end{array}} \\ ~~~ \begin{array}{l} \moveboundaries \end{array} \\ {\bf \color{blue} {endwhile}} \\ \hline \end{array} } \newcommand{\complexone}{ \begin{array}{|c|}\hline \!\pm\! \\ \hline \end{array}~ } \newcommand{\HQR}{{\rm HQR}} \newcommand{\QR}{{\rm QR}} \newcommand{\st}{{\rm \ s.t. }} \newcommand{\QRQ}{{\rm {\normalsize \bf Q}{\rm \tiny R}}} \newcommand{\QRR}{{\rm {\rm \tiny Q}{\bf \normalsize R}}} \newcommand{\deltaalpha}{\delta\!\alpha} \newcommand{\deltax}{\delta\!x} \newcommand{\deltay}{\delta\!y} \newcommand{\deltaz}{\delta\!z} \newcommand{\deltaw}{\delta\!w} \newcommand{\DeltaA}{\delta\!\!A} \newcommand{\meps}{\epsilon_{\rm mach}} \newcommand{\fl}[1]{{\rm fl( #1 )}} \newcommand{\becomes}{:=} \newcommand{\defrowvector}[2]{ \left(#1_0, #1_1, \ldots, #1_{#2-1}\right) } \newcommand{\tr}[1]{{#1}^T} \newcommand{\LUpiv}[1]{{\rm LU}(#1)} \newcommand{\maxi}{{\rm maxi}} \newcommand{\Chol}[1]{{\rm Chol}( #1 )} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \)

Subsection 0.1.1 Welcome

Linear algebra is one of the fundamental tools for computational and data scientists. In Advanced Linear Algebra: Foundations to Frontiers (ALAFF), you build your knowledge, understanding, and skills in linear algebra, practical algorithms for matrix computations, and how floating-point arithmetic, as performed by computers, affects correctness.

The materials are organized into Weeks that correspond to a chunk of information that is covered in a typical on-campus week. These weeks are arranged into three parts:

Part I: Orthogonality

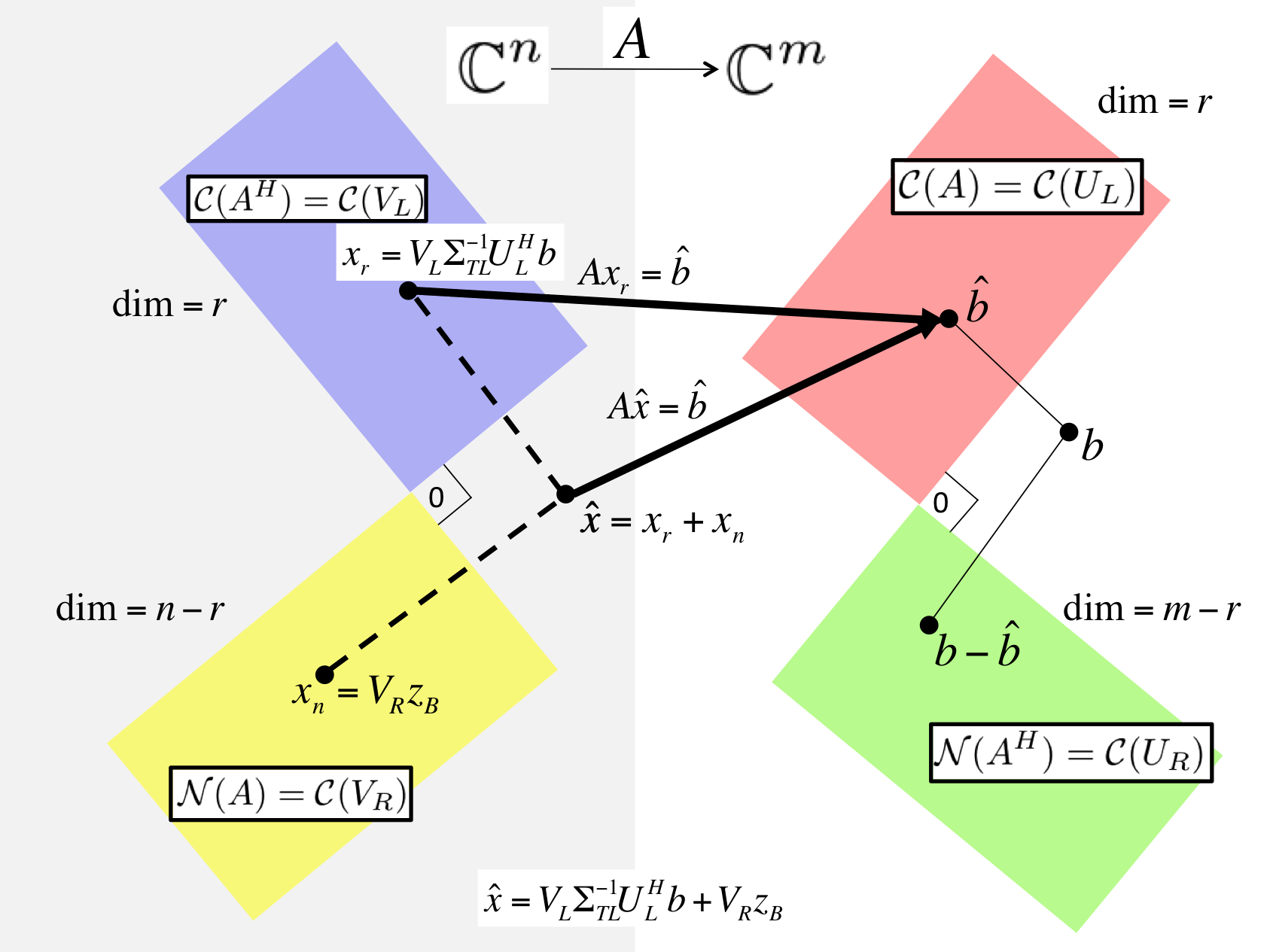
The Singular Value Decomposition (SVD) is possibly the most important result in linear algebra, yet too advanced to cover in an introductory undergraduate course. To be able to get to this topic as quickly as possible, we start by focusing on orthogonality, which is at the heart of image compression, Google's page rank algorithm, and linear least-squares approximation.

Part II: Solving Linear Systems

Solving linear systems, via direct or iterative methods, is at the core of applications in computational science and machine learning. We also leverage these topics to introduce numerical stability of algorithms: the classical study that qualifies and quantifies the "correctness" of an algorithm in the presence of floating point computation and approximation. Along the way, we discuss how to restructure algorithms so that they can attain high performance on modern CPUs.

Part III: Eigenvalues and Eigenvectors

Many problems in science have the property that if one looks at them in just the right way (in the right basis), they greatly simplify and/or decouple into simpler subproblems. Eigenvalue and eigenvectors are the key to discovering how to view a linear transformation, represented by a matrix, in that special way. Algorithms for computing them also are the key to practical algorithms for computing the SVD

In this week (Week 0), we walk you through some of the basic course information and help you set up for learning. The week itself is structured like future weeks, so that you become familiar with that structure.