Subsection 1.2.5 Unit ball
¶In 3-dimensional space, the notion of the unit ball is intuitive: the set of all points that are a (Euclidean) distance of one from the origin. Vectors have no position and can have more than three components. Still the unit ball for the 2-norm is a straight forward extension to the set of all vectors with length (2-norm) one. More generally, the unit ball for any norm can be defined:
Definition 1.2.5.1. Unit ball.
Given norm \(\| \cdot \| : \Cm \rightarrow \mathbb R \text{,}\) the unit ball with respect to \(\| \cdot \|\) is the set \(\{ x ~\vert ~ \| x \| = 1 \} \) (the set of all vectors with norm equal to one). We will use \(\| x \| = 1 \) as shorthand for \(\{ x ~\vert ~ \| x \| = 1 \} \text{.}\)
Homework 1.2.5.1.
Although vectors have no position, it is convenient to visualize a vector \(x \in \R^2 \) by the point in the plane to which it extends when rooted at the origin. For example, the vector \(x = \left( \begin{array}{c} 2 \\ 1 \end{array} \right) \) can be so visualized with the point \(( 2, 1 ) \text{.}\) With this in mind, match the pictures on the right corresponding to the sets on the left:
(a) \(\| x \|_2 = 1 \text{.}\)
(1)
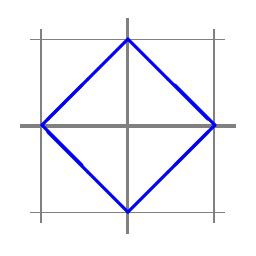
(b) \(\| x \|_1 = 1 \text{.}\)
(2)
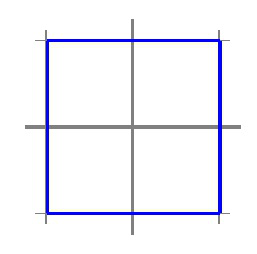
(c) \(\| x \|_\infty = 1 \text{.}\)
(3)
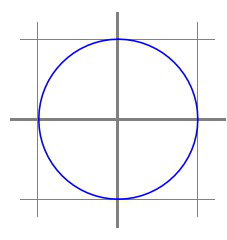
(a) \(\| x \|_2 = 1 \text{.}\)
(3)

(b) \(\| x \|_1 = 1 \text{.}\)
(1)

(c) \(\| x \|_\infty = 1 \text{.}\)
(2)

