Subsection 3.3.2 Householder transformation
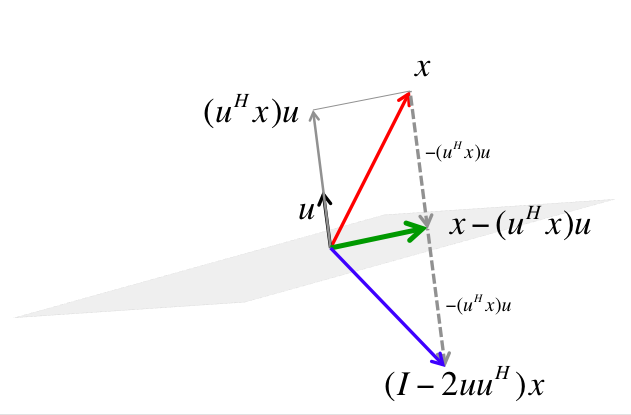
¶What we have discovered in this first video is how to construct a Householder transformation, also referred to as a reflector, since it acts like a mirroring with respect to the subspace orthogonal to the vector \(u \text{,}\) as illustrated in Figure 3.3.2.1.
PowerPoint source (Resources/Week03/HouseholderTransformation.pptx).
Definition 3.3.2.2.
Let \(u \in \Cn \) be a vector of unit length (\(\| u \|_2 = 1 \)). Then \(H = I - 2 u u^H \) is said to be a Householder transformation or (Householder) reflector.
We observe:
-
Any vector \(z \) that is perpendicular to \(u \) is left unchanged:
\begin{equation*} ( I - 2 u u^H ) z = z - 2 u ( u^H z ) = z . \end{equation*} -
Any vector \(x \) can be written as \(x = z + u^H x u \) where \(z \) is perpendicular to \(u \) and \(u^H x u \) is the component of \(x \) in the direction of \(u \text{.}\) Then
\begin{equation*} \begin{array}{rcl} ( I - 2 u u^H ) x \amp=\amp ( I - 2 u u^H ) ( z + u^H x u ) = z + u^H x u - 2 u \begin{array}[t]{c} \underbrace{u^H z} \\ 0 \end{array} - 2 u u^H u^H x u \\ \amp=\amp z + u^H x u - 2 u^H x \begin{array}[t]{c} \underbrace{u^H u}\\ 1 \end{array} u = z - u^H x u. \end{array} \end{equation*}
These observations can be interpreted as follows: The space perpendicular to \(u \) acts as a "mirror": a vector that is an element in that space (along the mirror) is not reflected. However, if a vector has a component that is orthogonal to the mirror, that component is reversed in direction, as illustrated in Figure 3.3.2.1. Notice that a reflection preserves the length of a vector.
Homework 3.3.2.1.
Show that if \(H \) is a reflector, then
\(H H = I \) (reflecting the reflection of a vector results in the original vector).
\(H = H^H \text{.}\)
\(H^H H = H H^H = I \) (a reflector is unitary).
Show that if \(H \) is a reflector, then
-
\(H H = I \) (reflecting the reflection of a vector results in the original vector).
Solution:
\begin{equation*} \begin{array}{l} ( I - 2 u u^H ) ( I - 2 u u^H ) \\ ~~~ = ~~~~ \\ I - 2 u u^H - 2 u u^H + 4 u \begin{array}[t]{c} \underbrace{ u^H u } \\ 1 \end{array} u^H\\ ~~~ = ~~~~ \\ I - 4 u u^H + 4 u u^H = I \end{array} \end{equation*} -
\(H = H^H \text{.}\)
Solution:
\begin{equation*} \begin{array}{l} ( I - 2 u u^H )^H\\ ~~~ = ~~~~ \\ I - 2 (u^H)^H u^H\\ ~~~ = ~~~~ \\ I - 2 u u^H \end{array} \end{equation*} -
\(H^H H = I \) (a reflector is unitary).
Solution:
\begin{equation*} \begin{array}{l} H^H H \\ ~~~ = ~~~~ \\ H H \\ ~~~ = ~~~~ \\ I \end{array} \end{equation*}

PowerPoint source (Resources/Week03/HouseholderTransformationAsUsed.pptx)
Next, let us ask the question of how to reflect a given \(x \in \Cn \) into another vector \(y \in \Cn \) with \(\| x \|_2 = \| y \|_2 \text{.}\) In other words, how do we compute vector \(u \) so that
From our discussion above, we need to find a vector \(u \) that is perpendicular to the space with respect to which we will reflect. From Figure 3.3.2.3 we notice that the vector from \(y \) to \(x \text{,}\) \(v = x - y \text{,}\) is perpendicular to the desired space. Thus, \(u \) must equal a unit vector in the direction \(v \text{:}\) \(u = {v}/{\| v \|_2} \text{.}\)
Remark 3.3.2.4.
In subsequent discussion we will prefer to give Householder transformations as \(I - u u^H /\tau \text{,}\) where \(\tau = {u^Hu}/{2} \) so that \(u \) needs no longer be a unit vector, just a direction. The reason for this will become obvious later.
When employing Householder transformations as part of a QR factorization algorithm, we need to introduce zeroes below the diagonal of our matrix. This requires a very special case of Householder transformation.
As we compute the QR factorization via Householder transformations, we will need to find a Householder transformation \(H \) that maps a vector \(x \) to a multiple of the first unit basis vector (\(e_0 \)). We discuss first how to find \(H \) in the case where \(x \in \Rn \text{.}\) We seek \(v \) so that \(( I - \frac{2}{v^T v} v v^T ) x = \pm \| x \|_2 e_0 \text{.}\) Since the resulting vector that we want is \(y = \pm \| x \|_2 e_0 \text{,}\) we must choose \(v = x - y = x \mp \| x \|_2 e_0 \text{.}\)
Example 3.3.2.5.
Show that if \(x \in \Rn \text{,}\) \(v = x \mp \| x \|_2 e_0 \text{,}\) and \(\tau = v^T v / 2 \) then \(( I - \frac{1}{\tau} v v^T ) x= \pm \| x \|_2 e_0 \text{.}\)
This is surprisingly messy... It is easier to derive the formula than it is to check it. So, we won't check it!
In practice, we choose \(v = x + \sign( \chi_1 ) \| x \|_2 e_0 \) where \(\chi_1 \) denotes the first element of \(x \text{.}\) The reason is as follows: the first element of \(v \text{,}\) \(\nu_1 \text{,}\) will be \(\nu_1 = \chi_1 \mp \| x \|_2 \text{.}\) If \(\chi_1 \) is positive and \(\| x \|_2 \) is almost equal to \(\chi_1 \text{,}\) then \(\chi_1 - \| x \|_2 \) is a small number and if there is error in \(\chi_1 \) and/or \(\| x \|_2 \text{,}\) this error becomes large relative to the result \(\chi_1 - \| x \|_2 \text{,}\) due to catastrophic cancellation. Regardless of whether \(\chi_1 \) is positive or negative, we can avoid this by choosing \(v = x + \sign( \chi_1 ) \| x \|_2 e_0 \text{:}\)
Remark 3.3.2.6.
This is a good place to clarify how we index in this course. Here we label the first element of the vector \(x \) as \(\chi_1 \text{,}\) despite the fact that we have advocated in favor of indexing starting with zero. In our algorithms that leverage the FLAME notation (partitioning/repartitioning), you may have noticed that a vector or scalar indexed with \(1 \) refers to the "current column/row" or "current element". In preparation of using the computation of the vectors \(v \) and \(u\) in the setting of such an algorithm, we use \(\chi_1\) here for the first element from which these vectors will be computed, which tends to be an element that is indexed with \(1 \text{.}\) So, there is reasoning behind the apparent insanity.
Ponder This 3.3.2.2.
Consider \(x \in \R^2 \) as drawn below:

Draw a vector \(\rho e_0 \) to which \(x \) is "mirrored."
Draw the line that "mirrors."
Draw the vector \(v \) from which \(u \) is computed.
Repeat for the "other" vector \(\rho e_0 \text{.}\)
Computationally, which choice of mirror is better than the other? Why?
