Subsection 4.6.2 Summary
¶The LLS problem can be states as: Given \(A \in \Cmxn \) and \(b \in \Cm \) find \(\hat x \in \Cn \) such that
Given \(A \in \Cmxn \text{,}\)
-
The column space, \(\Col( A ) \text{,}\) which is equal to the set of all vectors that are linear combinations of the columns of \(A \)
\begin{equation*} \{ y ~\vert~ y = A x \}. \end{equation*} -
The null space, \(\Null( A ) \text{,}\) which is equal to the set of all vectors that are mapped to the zero vector by \(A \)
\begin{equation*} \{ x ~\vert~ A x = 0 \}. \end{equation*} -
The row space, \(\Rowspace( A ) \text{,}\) which is equal to the set
\begin{equation*} \{ y ~\vert~ y^H = x^H A \}. \end{equation*}Notice that \(\Rowspace( A ) = \Col( A^H ) \text{.}\)
-
The left null space, which is equal to the set of all vectors
\begin{equation*} \{ x ~\vert~ x^H A = 0 \}. \end{equation*}Notice that this set is equal to \(\Null( A^H ) \text{.}\)
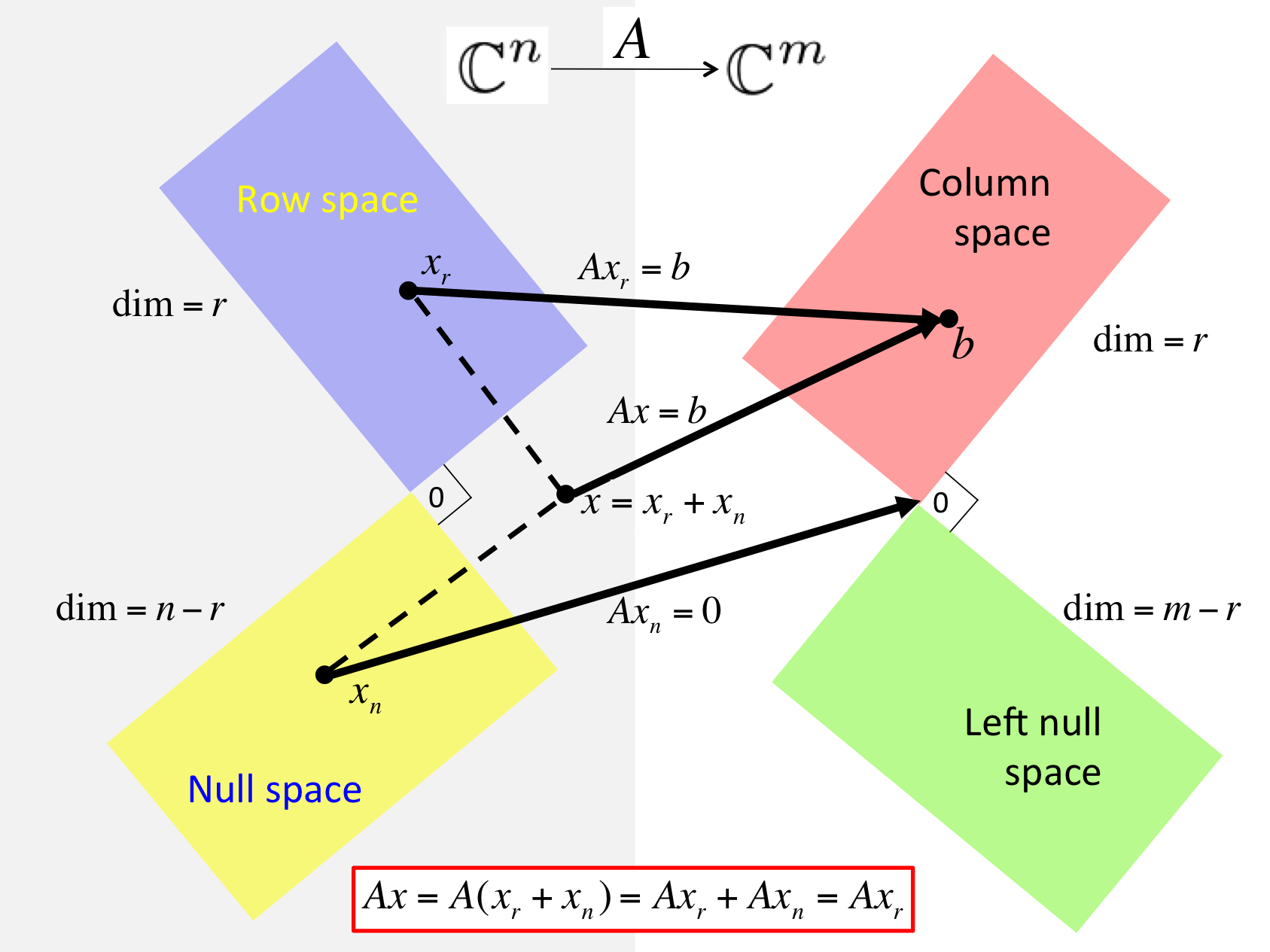
If \(A x = b \) then there exist \(x_r \in \Rowspace( A ) \) and \(x = x_r + x_n \) where \(x_r \in \Rowspace( A ) \) and \(x_n \in \Null( A ) \text{.}\)
These insights are summarized in the following picture, which also captures the orthogonality of the spaces.
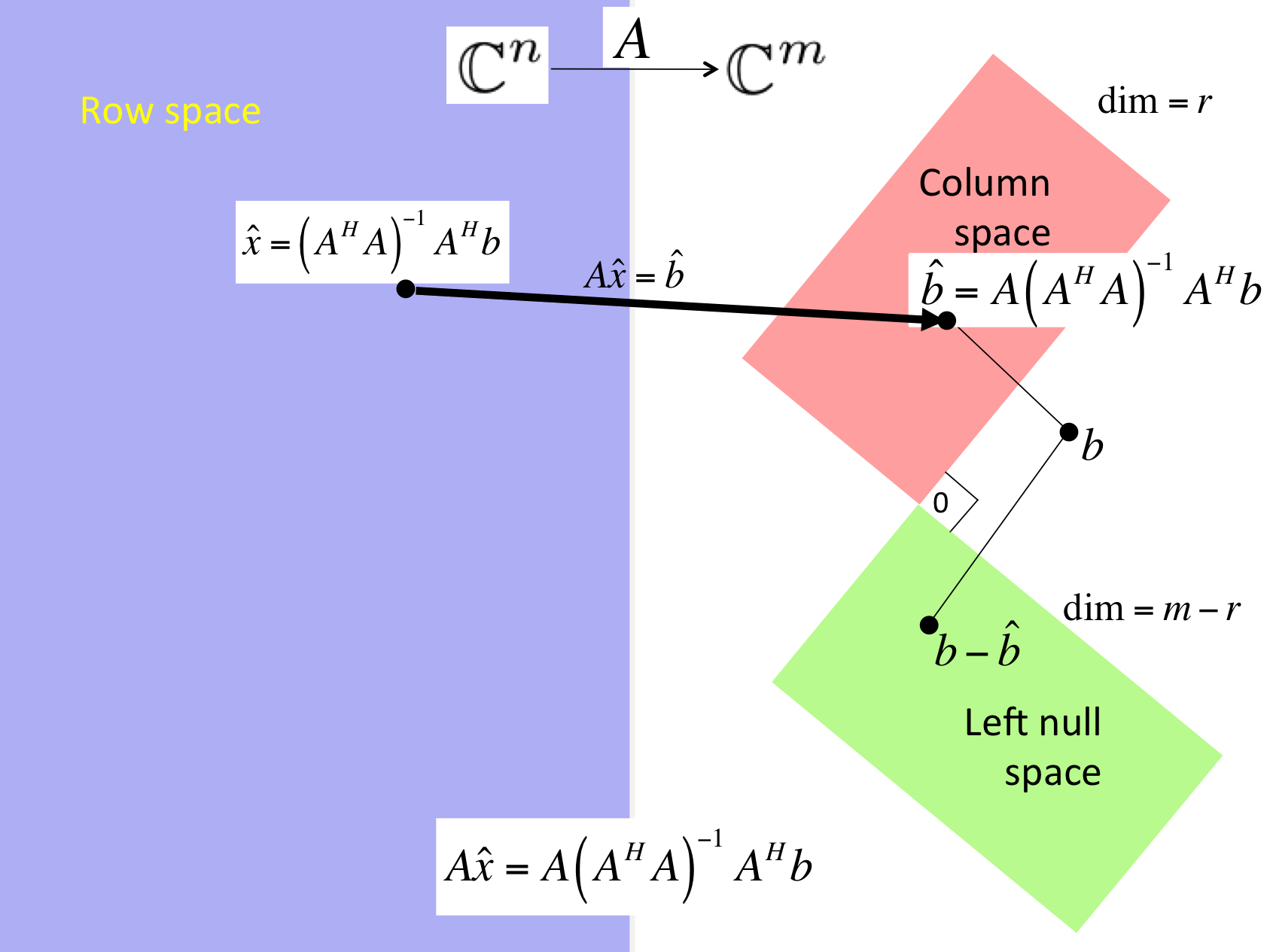
If \(A \) has linearly independent columns, then the solution of LLS, \(\widehat x \text{,}\) equals the solution of the normal equations
as summarized in
Definition 4.6.2.1. Condition number of matrix with linearly independent columns.
Let \(A \in \Cmxn \) have linearly independent columns (and hence \(n \leq m \)). Then its condition number (with respect to the 2-norm) is defined by
Assuming \(A \) has linearly independent columns, let \(\hat b = A \hat x \) where \(\hat b \) is the projection of \(b \) onto the column space of \(A \) (in other words, \(\hat x \) solves the LLS problem), \(\cos( \theta ) = \| \hat b \|_2 / \| b \|_2 \text{,}\) and \(\hat b + \delta\! \hat b = A ( \hat x + \delta\! \hat x ) \text{,}\) where \(\delta\! \hat b \) equals the projection of \(\delta\!b \) onto the column space of \(A \text{.}\) Then
captures the sensitivity of the LLS problem to changes in the right-hand side.
Theorem 4.6.2.2.
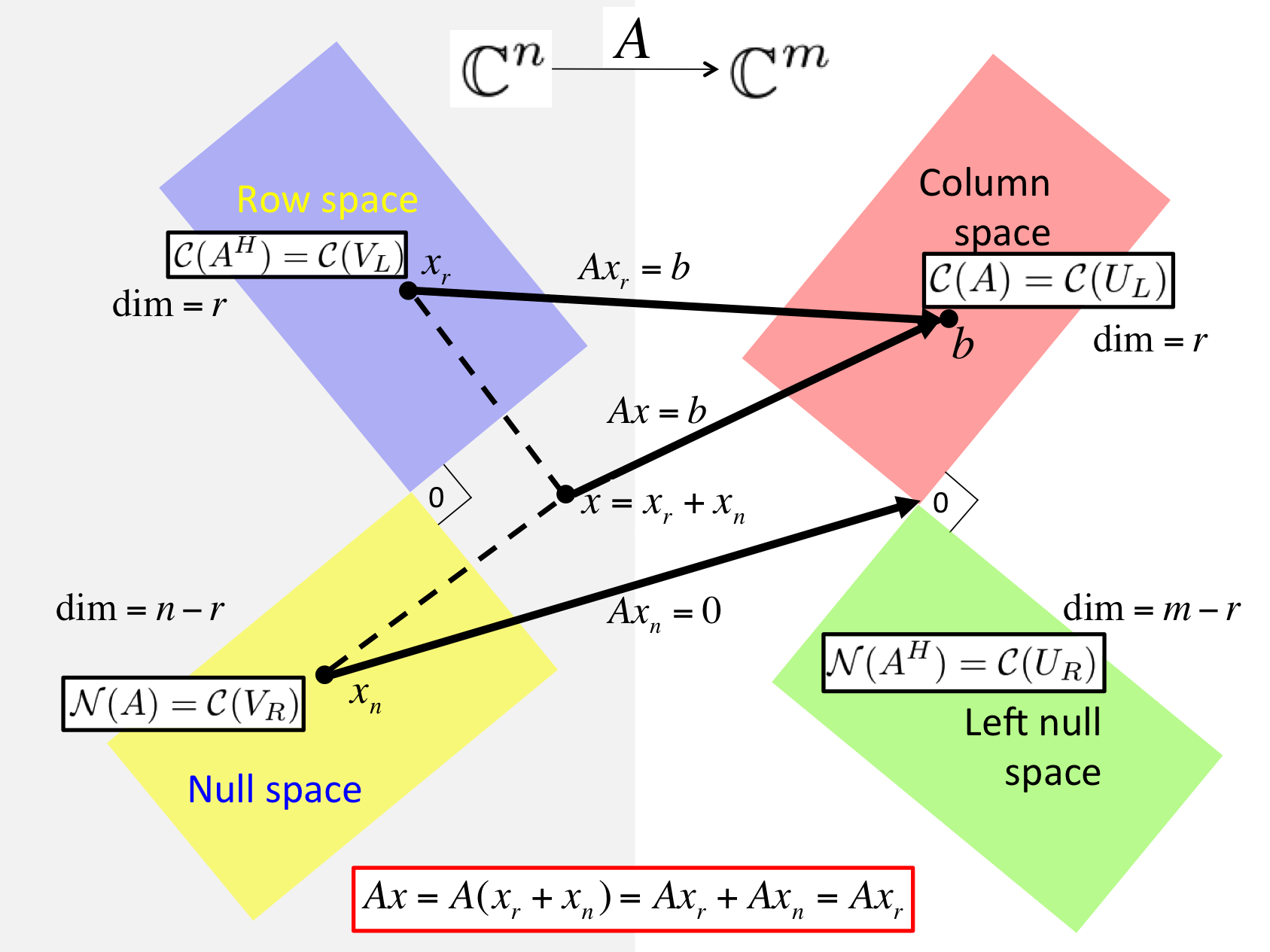
Given \(A \in \C^{m \times n}\text{,}\) let \(A = U_L \Sigma_{TL} V_L^H \) equal its Reduced SVD and \(A = \left( \begin{array}{c | c} U_L \amp U_R \end{array} \right) \left( \begin{array}{c | c} \Sigma_{TL} \amp 0 \\ \hline 0 \amp 0 \end{array} \right) \left( \begin{array}{c | c} V_L \amp V_R \end{array} \right)^H \) its SVD. Then
\(\Col( A ) = \Col( U_L ) \text{,}\)
\(\Null( A ) = \Col( V_R ) \text{,}\)
\(\Rowspace( A ) = \Col( A^H ) = \Col( V_L ) \text{,}\) and
\(\Null( A^H ) = \Col( U_R ) \text{.}\)
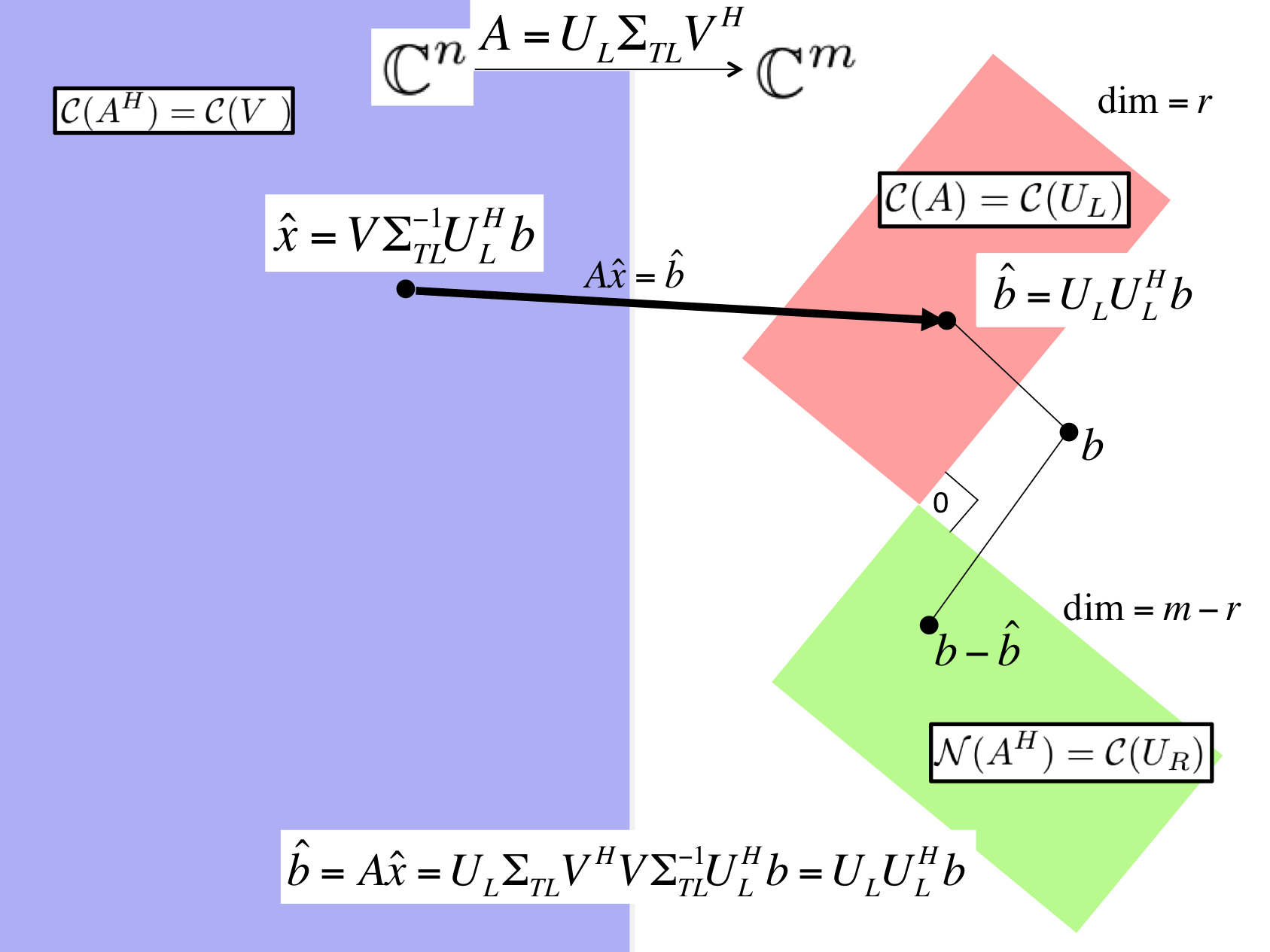
If \(A \) has linearly independent columns and \(A = U_L \Sigma_{TL} V_L^H \) is its Reduced SVD, then
solves LLS.
Given \(A \in \C^{m \times n}\text{,}\) let \(A = U_L \Sigma_{TL} V_L^H \) equal its Reduced SVD and \(A = \left( \begin{array}{c | c} U_L \amp U_R \end{array} \right) \left( \begin{array}{c | c} \Sigma_{TL} \amp 0 \\ \hline 0 \amp 0 \end{array} \right) \left( \begin{array}{c | c} V_L \amp V_R \end{array} \right)^H \) its SVD. Then
is the general solution to LLS, where \(z_b \) is any vector in \(\C^{n-r} \text{.}\)
Theorem 4.6.2.3.
Assume \(A \in \Cmxn \) has linearly independent columns and let \(A = Q R \) be its QR factorization with orthonormal matrix \(Q \in \Cmxn \) and upper triangular matrix \(R \in \Cnxn \text{.}\) Then the LLS problem
is solved by the unique solution of
Solving LLS via Gram-Schmidt QR factorization for \(A \in \Cmxn \text{:}\)
Compute QR factorization via (Classical or Modified) Gram-Schmidt: approximately \(2 m n^2 \) flops.
Compute \(y = Q^H b \text{:}\) approximately \(2 m n^2 \) flops.
Solve \(R \hat x = y \text{:}\) approximately \(n^2 \) flops.
Solving LLS via Householder QR factorization for \(A \in \Cmxn \text{:}\)
Householder QR factorization: approximately \(2 m n^2 - \frac{2}{3} n^3 \) flops.
Compute \(y_T = Q^H bnn \) by applying Householder transformations: approximately \(4 m n - 2 n^2 \) flops.
Solve \(R_{TL} \hat x = y_T \text{:}\) approximately \(n^2 \) flops.
