Skip to main content

Subsection 1.2.3 The vector 2-norm (Euclidean length)

The length of a vector is most commonly measured by the "square root of the sum of the squares of the elements," also known as the Euclidean norm. It is called the 2-norm because it is a member of a class of norms known as \(p\)-norms, discussed in the next unit.

Definition 1.2.3.1. Vector 2-norm.

The vector 2-norm \(\| \cdot \|_2 : \C^m \rightarrow \mathbb R \) is defined for \(x \in \C^m \) by

\begin{equation*} \| x \|_2 = \sqrt{ \vert \chi_0 \vert^2 + \cdots + \vert \chi_{m-1} \vert^2 } = \sqrt{\sum_{i=0}^{m-1} \vert \chi_i \vert^2} . \end{equation*}

Equivalently, it can be defined by

\begin{equation*} \| x \|_2 = \sqrt{x^H x} \end{equation*}

or

\begin{equation*} \| x \|_2 = \sqrt{ \overline \chi_0 \chi_0 + \cdots + \overline \chi_{m-1} \chi_{m-1} } = \sqrt{ \sum_{i=0}^{m-1} \overline \chi_i \chi_i }. \end{equation*}
Remark 1.2.3.2.

The notation \(x^H \) requires a bit of explanation. If

\begin{equation*} x = \left( \begin{array}{c} \chi_0 \\ \vdots \\ \chi_m \end{array} \right) \end{equation*}

then the row vector

\begin{equation*} x^H = \left( \begin{array}{c c c} \overline \chi_0 \amp \cdots \amp \overline \chi_m \end{array} \right) \end{equation*}

is the Hermitian transpose of \(x \) (or, equivalently, the Hermitian transpose of the vector \(x \) that is viewed as a matrix) and \(x^H y \) can be thought of as the dot product of \(x\) and \(y \) or, equivalently, as the matrix-vector multiplication of the matrix \(x^H \) times the vector \(y \text{.}\)

To prove that the 2-norm is a norm (just calling it a norm doesn't mean it is, after all), we need a result known as the Cauchy-Schwarz inequality. This inequality relates the magnitude of the dot product of two vectors to the product of their 2-norms: if \(x, y \in \R^m \text{,}\) then \(\vert x^T y \vert \leq \| x \|_2 \| y \|_2 \text{.}\) To motivate this result before we rigorously prove it, recall from your undergraduate studies that the component of \(x \) in the direction of a vector \(y \) of unit length is given by \((y^T x) y \text{,}\) as illustrated by

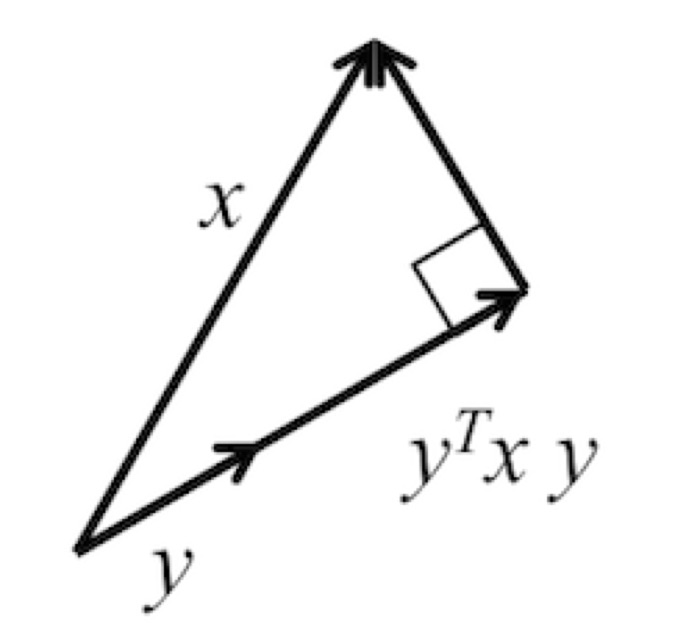
The length of the component of \(x \) in the direction of \(y \) then equals

\begin{equation*} \begin{array}{l} \| (y^T x) y \|_2 \\ ~~~~ = ~~~ \lt \mbox{ definition } \gt \\ \sqrt{ (y^T x)^T y^T ( y^T x ) y} \\ ~~~~ = ~~~ \lt z \alpha = \alpha z \gt \\ \sqrt{(x^T y)^2 y^T y } \\ ~~~~ = ~~~ \lt y \mbox{ has unit length } \gt \\ \vert y^T x \vert \\ ~~~~ = ~~~ \lt \mbox{ definition } \gt \\ \vert x^T y \vert. \end{array} \end{equation*}

Thus \(\vert x^T y \vert \leq \| x \|_2 \) (since a component should be shorter than the whole). If \(y \) is not of unit length (but a nonzero vector), then \(\vert x^T \frac{y}{ \| y \|_2} \vert \leq \| x \|_2 \) or, equivalently, \(\vert x^T y \vert \leq \| x \|_2 \| y \|_2\text{.}\)

We now state this result as a theorem, generalized to complex valued vectors:

Assume that \(x \neq 0 \) and \(y \neq 0 \text{,}\) since otherwise the inequality is trivially true. We can then choose \({\widehat x} = x / \| x \|_2 \) and \(\widehat {y} = y / \| y \|_2 \text{.}\) This leaves us to prove that \(\vert {\widehat x}^H \widehat y \vert \leq 1\) since \(\| {\widehat x} \|_2 = \| \widehat y \|_2 = 1 \text{.}\)

Pick

\begin{equation*} \alpha = \left\{ \begin{array}{ll} 1 \amp \mbox{ if } x^H y = 0 \\ \widehat y^H {\widehat x} / \vert {\widehat x}^H \widehat y \vert \amp \mbox{ otherwise.} \end{array} \right. \end{equation*}

so that \(\vert \alpha \vert = 1 \) and \(\alpha \widehat x^H \widehat y\) is real and nonnegative. Note that since it is real we also know that

\begin{equation*} \begin{array}{l} \alpha {\widehat x}^H \widehat y \\ ~~~=~~~~\lt \beta = \overline \beta \mbox{ if } \beta \mbox{ is real } \gt \\ \overline{ \alpha {\widehat x}^H \widehat y } \\ ~~~= ~~~~ \lt \mbox{ property of complex conjugation } \gt \\ \overline{\alpha} \widehat y^H {\widehat x} \end{array}\text{.} \end{equation*}

Now,

\begin{equation*} \begin{array}{l} 0 \\ ~~~\leq~~~~ \lt \| \cdot \|_2 \mbox{ is nonnegative definite } \gt \\ \| \widehat x - \alpha \widehat y \|_2^2 \\ ~~~ = ~~~~ \lt \| z \|_2^2 = z^H z \gt\\ ( \widehat x - \alpha \widehat y )^H ( {\widehat x} - \alpha \widehat y ) \\ ~~~= ~~~~ \lt \mbox{ multiplying out } \gt \\ {\widehat x}^H {\widehat x} - \overline \alpha \widehat y^H \widehat x - \alpha {\widehat x}^H \widehat y + \overline \alpha \alpha \widehat y^H \widehat y \\ ~~~ =~~~~ \lt \mbox{ above assumptions and observations } \gt \\ 1 - 2 \alpha {\widehat x}^H \widehat y + \vert \alpha \vert^2 \\ ~~~ =~~~~ \lt \alpha {\widehat x}^H \widehat y = \vert {\widehat x}^H \widehat y \vert ; \vert \alpha \vert = 1\gt \\ 2 - 2 \vert {\widehat x}^H \widehat y \vert. \end{array} \end{equation*}

Thus \(\vert {\widehat x}^H \widehat y \vert \leq 1 \) and therefore \(\vert x^H y \vert \leq \| x\|_2 \| y \|_2 \text{.}\)

The proof of Theorem 1.2.3.3 does not employ any of the intuition we used to motivate it in the real valued case just before its statement. We leave it to the reader to prove the Cauchy-Schartz inequality for real-valued vectors by modifying (simplifying) the proof of Theorem 1.2.3.3.

Ponder This 1.2.3.1.

Let \(x, y \in \R^m \text{.}\) Prove that \(\vert x^T y \vert \leq \| x \|_2 \| y \|_2\) by specializing the proof of Theorem 1.2.3.3.

The following theorem states that the 2-norm is indeed a norm:

We leave its proof as an exercise.

Homework 1.2.3.2.
Prove Theorem 1.2.3.4.
Solution

To prove this, we merely check whether the three conditions are met:

Let \(x, y \in \C^m \) and \(\alpha \in \mathbb C \) be arbitrarily chosen. Then

  • \(x \neq 0 \Rightarrow \| x \|_2 > 0 \) (\(\| \cdot \|_2 \) is positive definite):

    Notice that \(x \neq 0 \) means that at least one of its components is nonzero. Let's assume that \(\chi_j \neq 0 \text{.}\) Then

    \begin{equation*} \| x \|_2 = \sqrt{ \vert \chi_0 \vert^2 + \cdots + \vert \chi_{m-1} \vert^2 } \geq \sqrt{ \vert \chi_j \vert^2 } = \vert \chi_j \vert > 0 . \end{equation*}

  • \(\| \alpha x \|_2 = \vert \alpha \vert \| x \|_2 \) (\(\| \cdot \|_2 \) is homogeneous):

    \begin{equation*} \begin{array}{l} \| \alpha x \|_2 \\ ~~~=~~~~ \lt \mbox{ scaling a vector scales its components; definition} \gt \\ \sqrt{ \vert \alpha \chi_0 \vert^2 + \cdots + \vert \alpha \chi_{m-1} \vert^2 } \\ ~~~=~~~~\lt { algebra} \gt \\ \sqrt{ \vert \alpha \vert^2 \vert \chi_0 \vert^2 + \cdots + \vert \alpha \vert^2 \vert \chi_{m-1} \vert^2 } \\ ~~~=~~~~\lt \mbox{ algebra} \gt \\ \sqrt{ \vert \alpha \vert^2 ( \vert \chi_0 \vert^2 + \cdots + \vert \chi_{m-1} \vert^2 ) } \\ ~~~=~~~~\lt \mbox{ algebra} \gt \\ \vert \alpha \vert \sqrt { \vert \chi_0 \vert^2 + \cdots + \vert \chi_{m-1} \vert^2 } \\ ~~~=~~~~\lt \mbox{ definition} \gt \\ \vert \alpha \vert \| x \|_2 . \end{array} \end{equation*}

  • \(\| x + y \|_2 \leq \| x \|_2 + \| y \|_2 \) (\(\| \cdot \|_2 \) obeys the triangle inequality):

    \begin{equation*} \begin{array}{lcl} \| x + y \|_2^2 \\ ~~~=~~~~\lt \| z \|_2^2 = z^H z \gt \\ ( x + y )^H ( x + y ) \\ ~~~=~~~~\lt \mbox{ distribute} \gt \\ x^H x + y^H x + x^H y + y^H y \\ ~~~=~~~~\lt \overline \beta + \beta = 2 \mbox{Real}( \beta ) \gt \\ x^H x +2 \mbox{Real}( x^H y ) + y^H y \\ ~~~\leq ~~~~\lt \mbox{ algebra } \gt \\ x^H x + 2\vert \mbox{Real}( x^H y ) \vert + y^H y \\ ~~~\leq~~~~ \lt \mbox{ algebra} \gt \\ x^H x + 2 \vert x^H y \vert + y^H y \\ ~~~\leq ~~~~ \lt \mbox{ algebra; Cauchy-Schwarz} \gt \\ \| x \|_2^2 + 2 \| x \|_2 \| y \|_2 + \| y \|_2^2 \\ ~~~ = ~~~~\lt \mbox{ algebra} \gt \\ ( \| x \|_2 + \| y \|_2 )^2. \end{array} \end{equation*}

    Taking the square root (an increasing function that hence maintains the inequality) of both sides yields the desired result.

Throughout this course, we will reason about subvectors and submatrices. Let's get some practice:

Homework 1.2.3.3.

Partition \(x \in \Cm \) into subvectors:

\begin{equation*} x = \left( \begin{array}{c} x_0 \\ \hline x_1 \\ \hline \vdots \\ \hline x_{M-1} \end{array} \right). \end{equation*}

ALWAYS/SOMETIMES/NEVER: \(\| x_i \|_2 \leq \| x \|_2 \text{.}\)

Answer

ALWAYS

Now prove it!

Solution
\begin{equation*} \begin{array}{l} \| x \|_2^2 \\ ~~~=~~~~ \lt \mbox{ partition vector } \gt \\ \left\| \left( \begin{array}{c} x_0 \\ \hline x_1 \\ \hline \vdots \\ \hline x_{M-1} \end{array} \right) \right\|_2^2 \\ ~~~=~~~~ \lt \mbox{ equivalent definition } \gt \\ \left( \begin{array}{c} x_0 \\ \hline x_1 \\ \hline \vdots \\ \hline x_{M-1} \end{array} \right)^H \left( \begin{array}{c} x_0 \\ \hline x_1 \\ \hline \vdots \\ \hline x_{M-1} \end{array} \right) \\ ~~~ = ~~~~ \lt \mbox{ dot product of partitioned vectors } \gt \\ x_0^H x_0 + x_1^H x_1 + \cdots + x_{M-1}^H x_{M-1} \\ ~~~ = ~~~ \lt \mbox{ equivalent definition } \gt \\ \| x_0 \|_2^2 + \| x_1 \|_2^2 + \cdots + \| x_{M-1} \|_2^2 \\ ~~~ \geq ~~~~ \lt \mbox{ algebra } \gt \\ \| x_i \|_2^2 \end{array} \end{equation*}

so that \(\| x_i \|_2^2 \leq \| x \|_2^2 \text{.}\) Taking the square root of both sides shows that \(\| x_i \|_2 \leq \| x \|_2.\)

login