Subsection 7.1.1 Where do sparse linear systems come from?
¶Many computational engineering and science applications start with some law of physics that applies to some physical problem. This is mathematically expressed as a Partial Differential Equation (PDE). We here will use one of the simplest of PDEs, Poisson's equation on the domain \(\Omega \) in two dimensions:
In two dimensions this is alternatively expressed as
with Dirichlet boundary condition \(\partial \Omega = 0 \) (meaning that \(u(x,y) = 0 \) on the boundary of domain \(\Omega \)). For example, the domain may be the square \(0\leq x,y \leq 1 \text{,}\) \(\partial \Omega \) its boundary, and the question may be a membrane with \(f \) being some load from, for example, a sound wave.
Since this course does not require a background in the mathematics of PDEs, let's explain the gist of all this in layman's terms.
We want to find the function \(u \) that satisfies the conditions specified by (7.1.1). It is assumed that \(u \) is appropriately differentiable.
For simplicity, let's assume the domain is the square with \(0 \leq x \leq 1 \) and \(0 \leq y \leq 1 \) so that the boundary \(\Omega \) is the boundary of this square. We assume that on the boundary the function equals zero.
It is usually difficult to analytically determine the continuous function \(u \) that solves such a "boundary value problem" (except for very simple examples).
To solve the problem computationally, the problem is "discretized". What this means for our example is that a mesh is laid over the domain, values for the function \(u \) at the mesh points are approximated, and the operator is approximated. In other words, the continuous domain is viewed as a mesh instead, as illustrated in Figure 7.1.1.1 (Left). We will assume an \(N \times N \) mesh of equally spaced points, where the distance between two adjacent points is \(h = 1/(N+1) \text{.}\) This means the mesh consists of points \(\{ ( \chi_i, \psi_j ) \}\) with \(\chi_i = (i+1)h \) for \(i = 0, 1, \ldots , N-1 \) and \(\psi_j = (j+1)h \) for \(j = 0, 1, \ldots , N-1 \text{.}\)
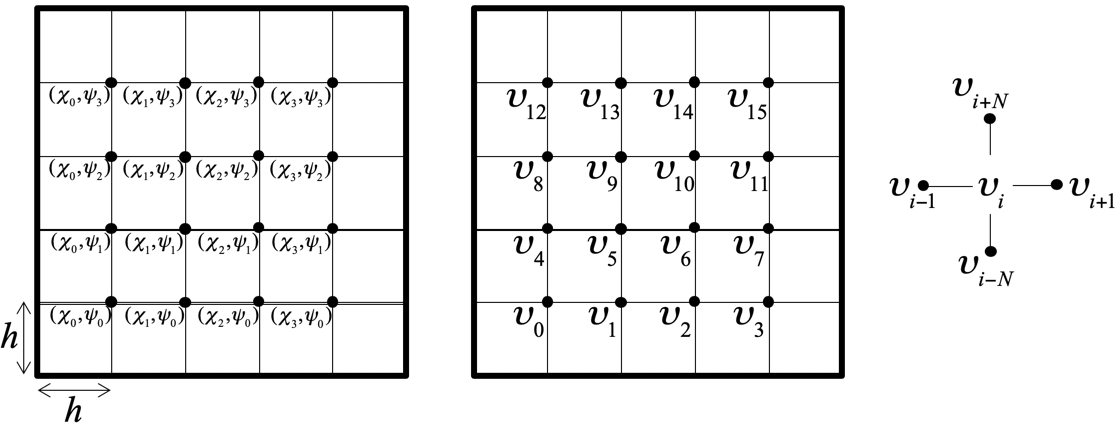
Figure 7.1.1.1. 2D mesh. -
If you do the math, details of which can be found in Subsection 7.4.1, you find that the problem in (7.1.1) can be approximated with a linear equation at each mesh point:
\begin{equation*} \frac{-u( \chi_{i}, \psi_{j-1} ) - u( \chi_{i-1},\psi_j ) + 4 u( \chi_i, \psi_j ) - u( x_{i+1}, \psi_j ) - u( x_{i}, \psi_{j+1} )}{h^2} = f( \chi_i, \psi_i ). \end{equation*}The values in this equation come from the "five point stencil" illustrated in Figure 7.1.1.1 (Right).
-
If we number the values at the grid points, \(u( \chi_i, \psi_j ) \) in what is called the "natural ordering" as illustrated in Figure 7.1.1.1 (Middle), then we can write all these insights, together with the boundary condition, as
\begin{equation*} - \upsilon_{i-N} - \upsilon_{i-1} + 4\upsilon_{i} - \upsilon_{i+1} - \upsilon_{i+N} = h^2 \phi_{i} \end{equation*}or, equivalently,
\begin{equation*} \upsilon_{i} = \frac{h^2 \phi_{i} + \upsilon_{i-N} + \upsilon_{i-1} + \upsilon_{i+1} + \upsilon_{i+N}}{4} \end{equation*}with appropriate modifications for the case where \(i\) places the point that yielded the equation on the bottom, left, right, and/or top of the mesh.
where \(\phi_{i} = f( \chi_i, \psi_j ) \) if \(( \chi_i, \psi_j ) \) is the point associated with value \(\upsilon_{i} \text{.}\) In matrix notation this becomes
This demonstrates how solving the discretized Poisson's equation boils down to the solution of a linear system \(A u = h^2 f \text{,}\) where \(A \) has a distinct sparsity pattern (pattern of nonzeroes).
Homework 7.1.1.1.
The observations in this unit suggest the following way of solving (7.1.1):
Discretize the domain \(0 \leq \chi, \psi \leq 1 \) by creating an \((N+2) \times (N+2) \) mesh of points.
An \((N+2) \times (N+2) \) array
Uholds the values \(u( \chi_i, \psi_i ) \) plus the boundary around it.Create an \((N+2) \times (N+2) \) array \(F \) that holds the values \(f( \chi_i, \psi_j ) \) (plus, for convenience, extra values that correspond to the boundary).
Set all values in \(U \) to zero. This initializes the last rows and columns to zero, which captures the boundary condition, and initializes the rest of the values at the mesh points to zero.
-
Repeatedly update all interior points with the formula
\begin{equation*} \begin{array}{l} U( i,j ) = \\ ( h^2 \begin{array}[t]{c} \underbrace{ F( i,j )} \\ f( \chi_i, \psi_{j} ) \end{array} + \begin{array}[t]{c} \underbrace{ U( i,j-1) }\\ u( \chi_i, \psi_{j-1} ) \end{array} + \begin{array}[t]{c} \underbrace{ U( i-1,j) }\\ u( \chi_{i-1}, \psi_{j} ) \end{array} + \begin{array}[t]{c} \underbrace{ U( i+1,j ) } \\ u( \chi_{i+1}, \psi_{j} ) \end{array} + \begin{array}[t]{c} \underbrace{ U( i,j+1 ) } \\ u( \chi_{i}, \psi_{j+1} ) \end{array} ) / {4} \end{array} \end{equation*}until the values converge.
Bingo! You have written your first iterative solver for a sparse linear system.
Test your solver with the problem where \(f( \chi, \psi ) = ( \alpha^2 + \beta^2 ) \pi^2 \sin( \alpha \pi \chi ) \sin( \beta \pi \psi ) \text{.}\)
Hint: if x and y are arrays with the vectors \(x \) and \(y \) (with entries \(\chi_i \) and \(\psi_j \)), then mesh( x, y, U ) plots the values in U.
Remark 7.1.1.2.
In Homework 7.2.1.4 we store the vectors \(u \) and \(f \) as they appear in Figure 7.1.1.1 as 2D arrays. This captures the fact that a 2d array of numbers isn't necessarily a matrix. In this case, it is a vector that is stored as a 2D array because it better captures how the values to be computed relate to the physical problem from which they arise.
Remark 7.1.1.3.
The point of this launch is that many problems that arise in computational science require the solution to a system of linear equations \(A x= b \) where \(A \) is a (very) sparse matrix. Often, the matrix does not even need to be explicitly formed and stored.
Remark 7.1.1.4.
Wilkinson defined a sparse matrix as any matrix with enough zeros that it pays to take advantage of them.
The problem used to motivate in this unit were suggested to us by Isaac Lee. You may enjoy other materials of his by visiting https://crunchingnumbers.live/2017/07/09/iterative-methods-part-2/.
