Subsection 12.2.4 Optimizing matrix-matrix multiplication, the real story
¶High-performance implementations of matrix-matrix multiplication (and related operations) block the computation for multiple levels of caches. This greatly reduces the overhead related to data movement between memory layers. In addition, at some level the implementation pays very careful attention to the use of vector registers and vector instructions so as to leverage parallelism in the architecture. This allows multiple floating point operations to be performed simultaneous within a single processing core, which is key to high performance on modern processors.
Current high-performance libraries invariably build upon the insights in the paper
[53] Kazushige Goto and Robert van de Geijn, Anatomy of High-Performance Matrix Multiplication, ACM Transactions on Mathematical Software, Vol. 34, No. 3: Article 12, May 2008.
This paper is generally considered a "must read" paper in high-performance computing. The techniques in that paper were "refactored" (carefully layered so as to make it more maintainable) in BLIS, as described in
[56] Field G. Van Zee and Robert A. van de Geijn, BLIS: A Framework for Rapidly Instantiating BLAS Functionality, ACM Journal on Mathematical Software, Vol. 41, No. 3, June 2015.
The algorithm described in both these papers can be captured by the picture in Figure 12.2.4.1.
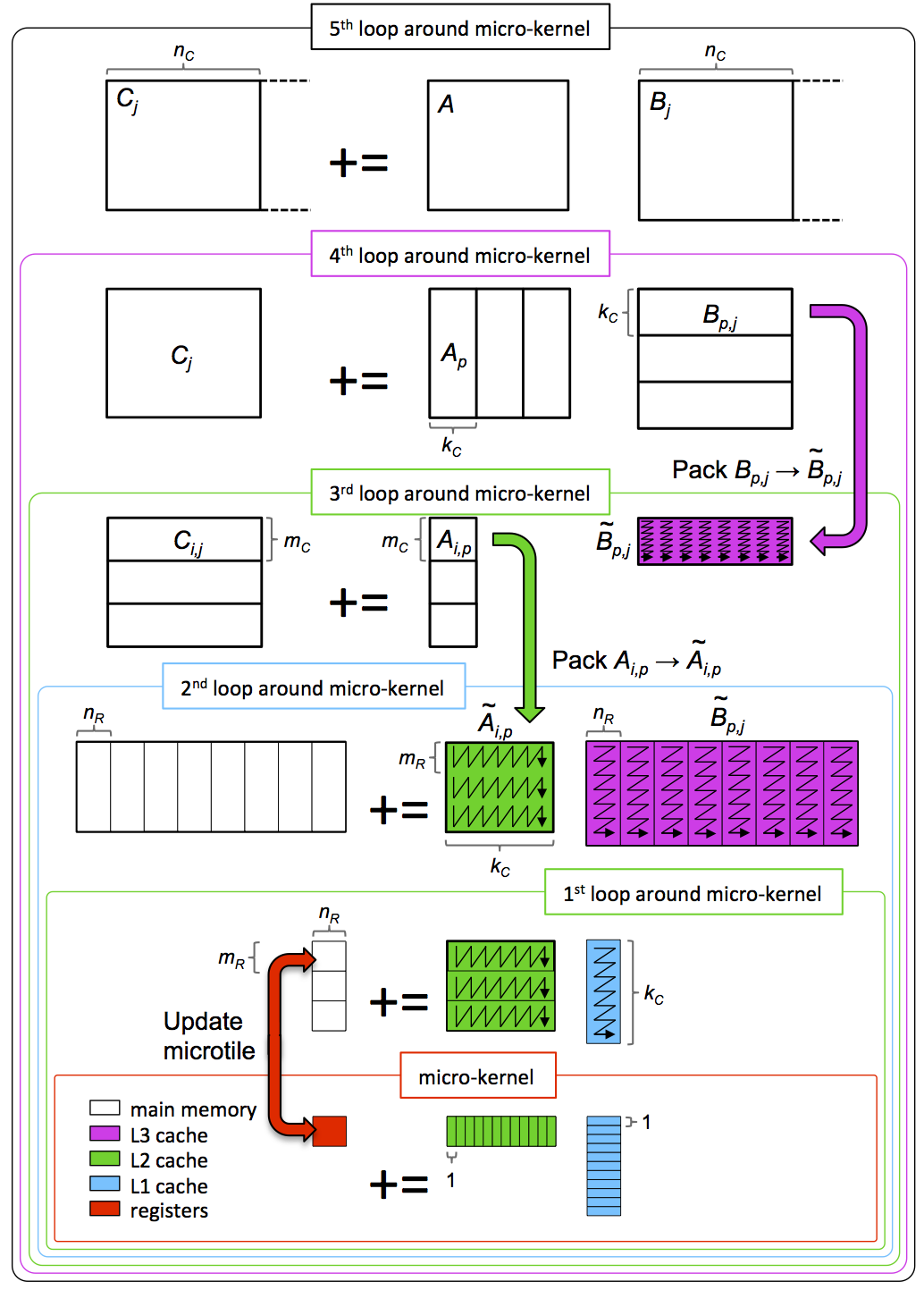
Picture adapted from [55]. Click to enlarge. PowerPoint source (step-by-step).
This is not the place to go into great detail. Once again, we point out that the interested learner will want to consider our Massive Open Online Course titled "LAFF-On Programming for High Performance" [42]. In that MOOC, we illustrate issues in high performance by exploring how high performance matrix-matrix multipication is implemented in practice.
