Subsection 12.5.2 Summary
¶This chapter highlights a few things that may serve you well:
How your computation accesses data and how it reuses data is of crucial importance if high performance is to be attained.
Compilers are typically not sophisticated enough to automagically transform a simple implementation into a high-performance implementation. You experienced this for the Gnu C compiler (gcc). It should be noted that some commercial compilers, for example Intel's icc compiler, does much better than a typical open source compiler.
The memory hierarchy of a modern CPU can be visualized as a pyramid:
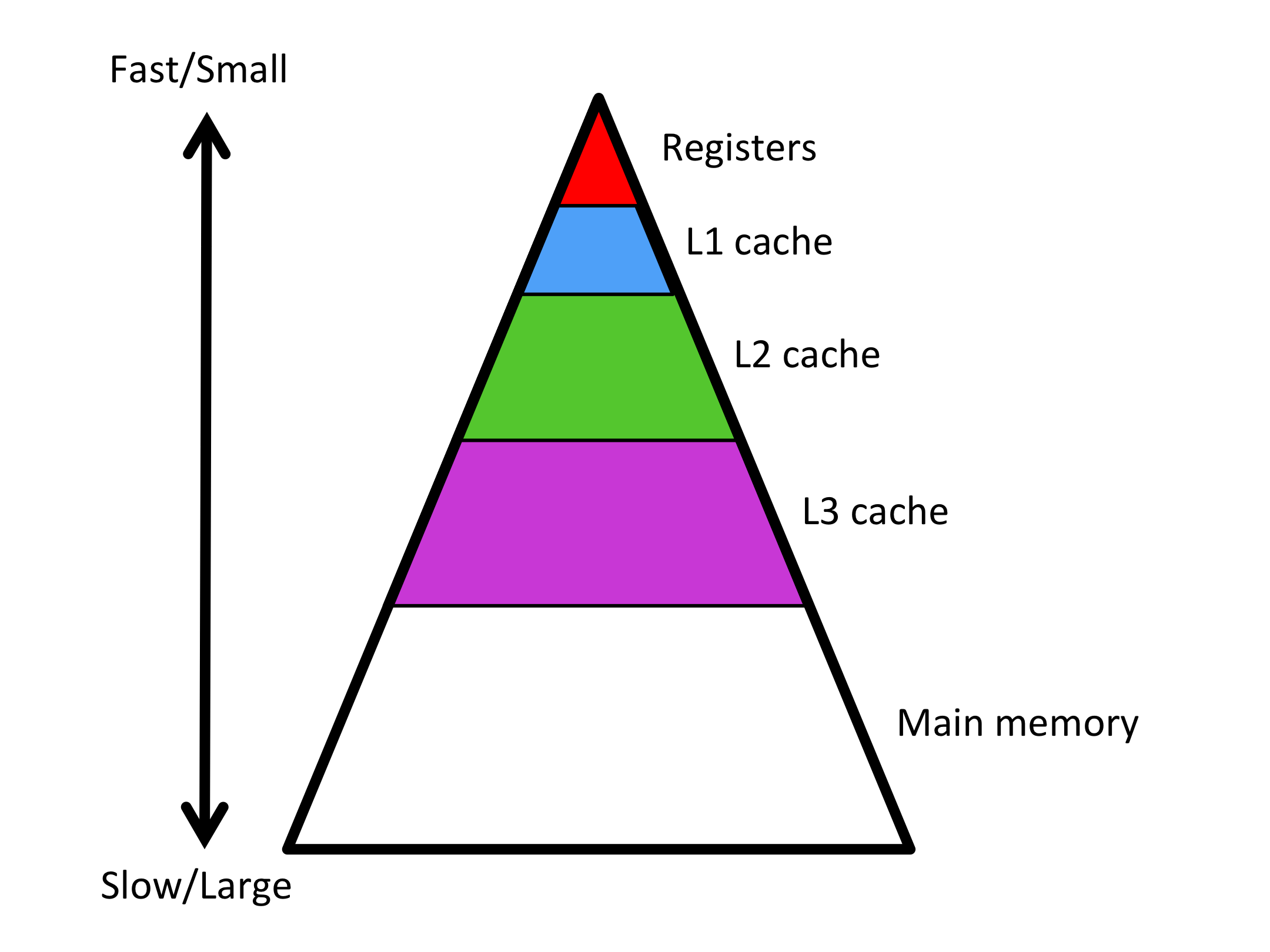
At the top, there are a few registers where data must reside before the floating point unit of the processor can compute on that data. Accessing data that are in registers is fast.
At the bottom, we depict the main memory of the processor. It typically takes orders of magnitude more time to bring data in from main memory than it takes to computer with that data. The main memory of a modern processor is very large.
In between are cache memories. The higher level the cache, the larger that cache can be and the longer it takes for the data to reach the registers.
To achieve high performance, the name of the game is to move data into an appropriate layer of the cache and to then reuse that data for many computations so as to amortize the cost of the movement of the data.
Optimizing the performance requires a combination of techniques:
If possible, at the low level computation must take advantage of instruction-level parallelism.
As mentioned above, to overcome long access times to memory, data that is moved between memory layers needs to be reused.
Data locality is important: accessing data that is contiguous in memory typically benefits performance.
Some operations exhibit an opportunity for reuse of data while others don't.
When computing a "vector-vector" operation, like a dot product or axpy operation, there is little opportunity for reuse of data: A computation with vectors of size \(m \) involves \(O( m ) \) computation with \(O( m ) \) data.
When computing a "matrix-vector" operation, like a matrix-vector multiplication or rank-1 update, there is still little opportunity for reuse of data: Such computation with matrices of size \(m \times m \) involves \(O( m^2 ) \) computation with \(O( m^2 ) \) data.
When computing a "matrix-matrix" operation, like a matrix-matrix multiplication, there is considerable opportunity for reuse of data: Such computation with matrices of size \(m \times m \) involves \(O( m^3 ) \) computation with \(O( m^2 ) \) data.
In order to facilitate portable high performance, the computational science community proposed an interface, the Basic Linear Algebra Subprograms (BLAS), for basic linear algebra functionality. The idea was that by standardizing such an interface, the community could expect that computer and third party software vendors would provide high-performance implementations of that interface. Much scientific and, increasingly, data science software is implemented in terms of the BLAS.
Rather than painstakingly implementing higher-level functionality, like LU factorization with pivoting or QR factorization, at a low level in order to improve the ratio of computation to memory operations, libraries like LAPACK formulate their implementations so that most computation is performed in a matrix-matrix operation. This retains most of the benefit of reuse of data without the need to reimplement such functionality when new architectures come along.
The opportunity for reusing data is much less for operations that involve sparse matrices.
