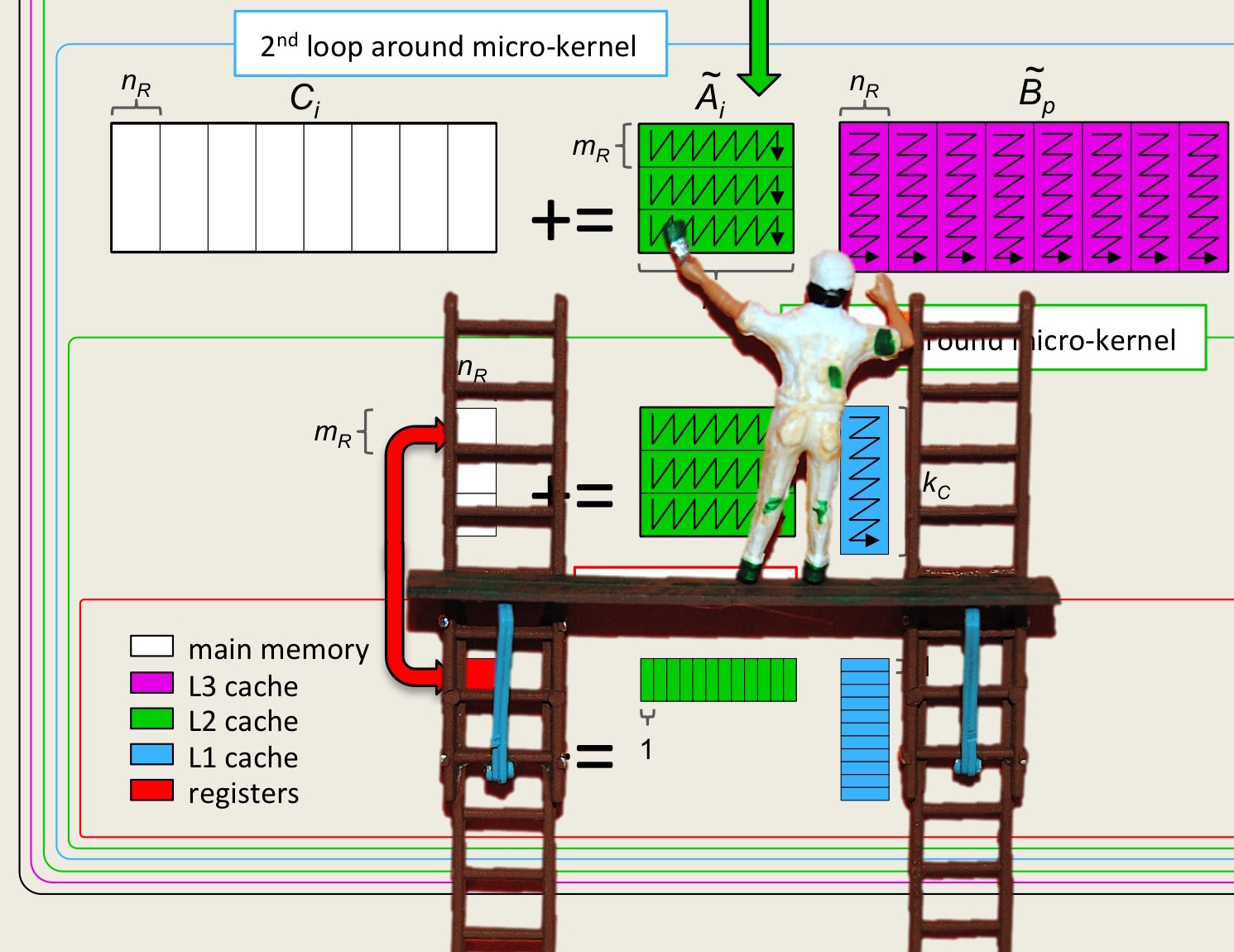
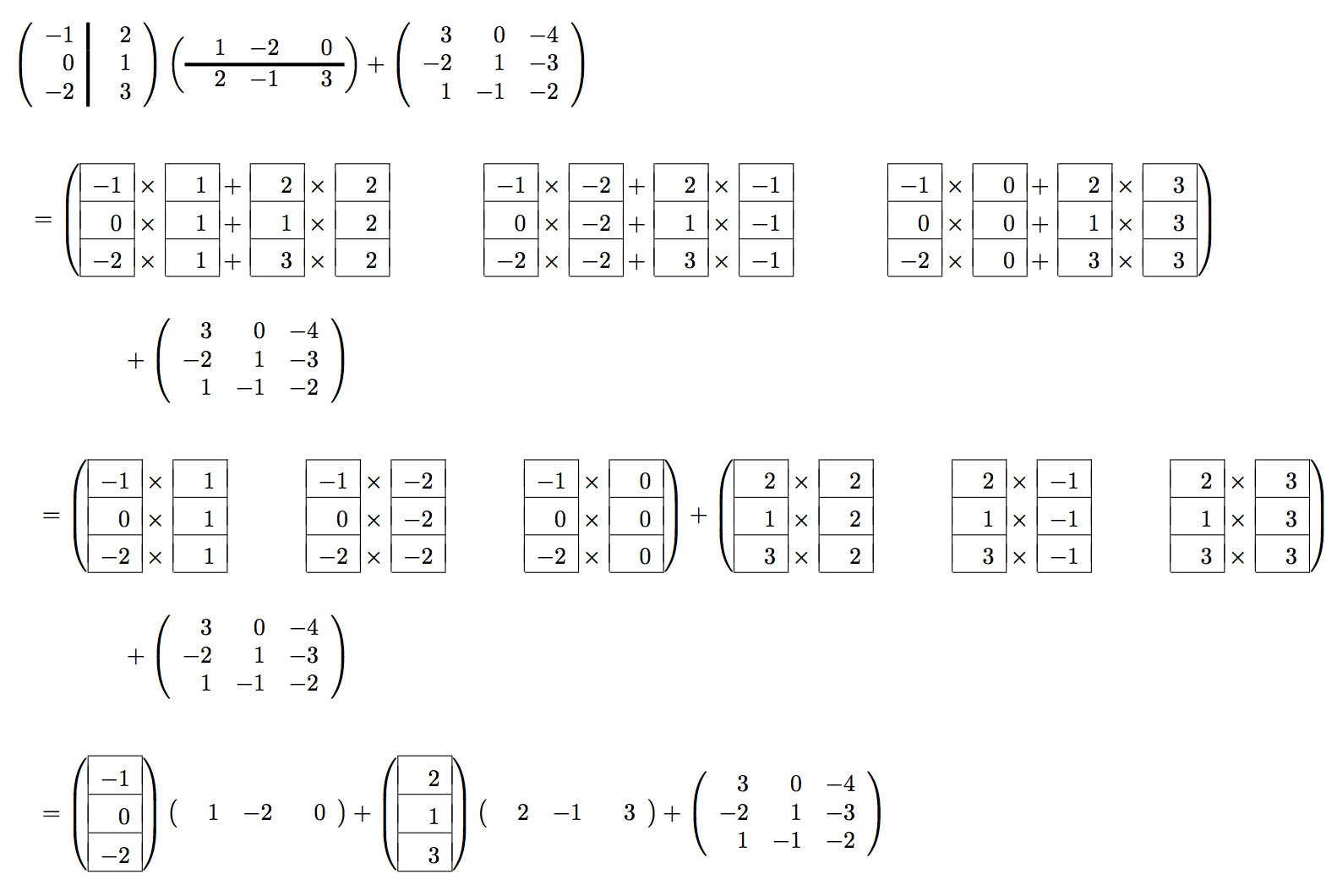Skip to main content

Unit 1.4.2 Matrix-matrix multiplication via rank-1 updates

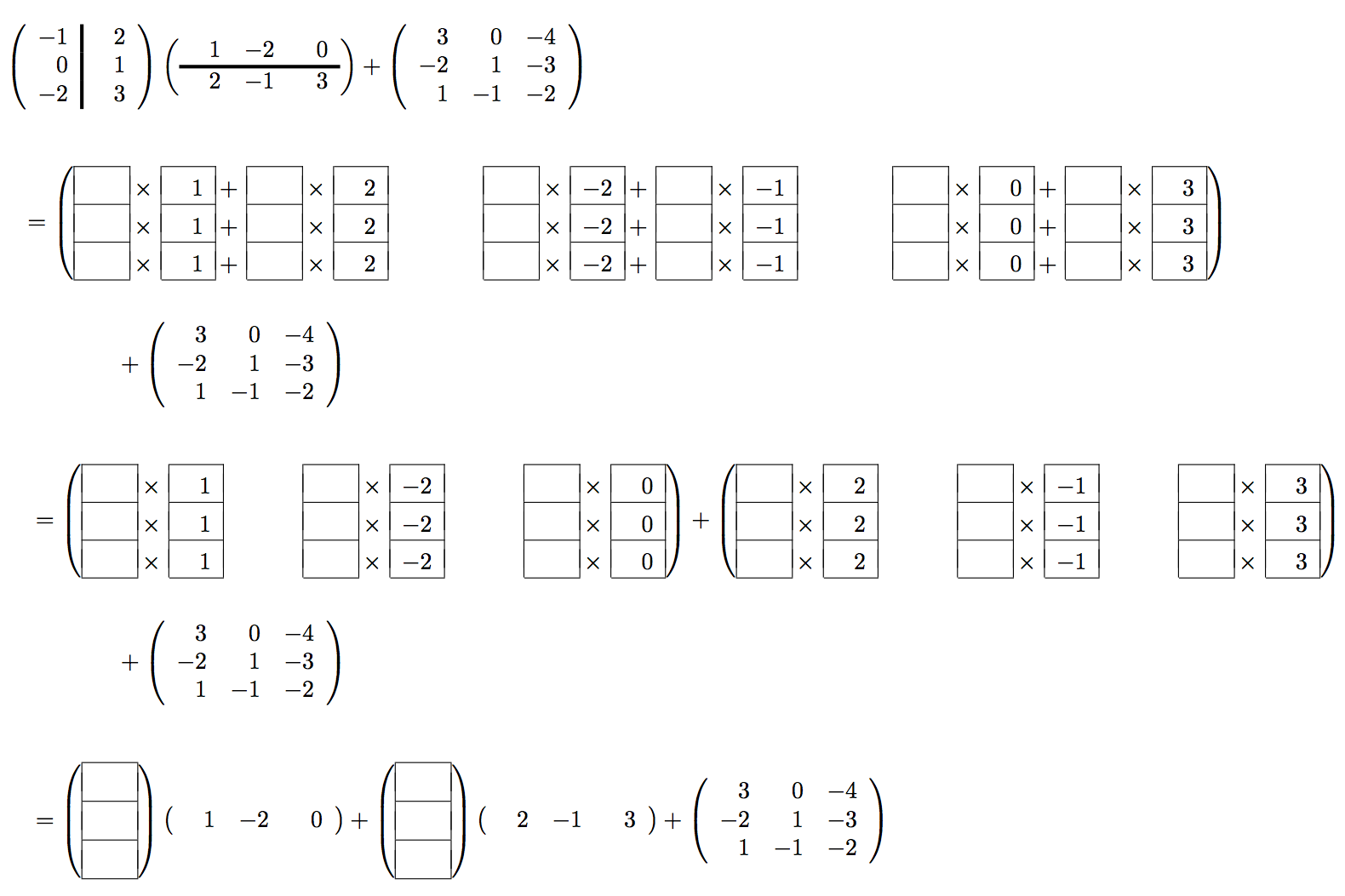
Let us partition \(A \) by columns and \(B \) by rows, so that

\begin{equation*} \begin{array}{rcl} C \amp:=\amp \left( \begin{array}{c | c | c | c } a_0 \amp a_1 \amp \cdots \amp a_{k-1} \end{array} \right) \left( \begin{array}{c} \widetilde b_0^T \\ \hline \widetilde b_1^T \\ \hline \vdots \\ \hline \widetilde b_{k-1}^T \end{array} \right) + C \\ \amp = \amp a_0 \widetilde b_0^T + a_1 \widetilde b_1^T +\cdots + a_{k-1} \widetilde b_{k-1}^T + C \end{array} \end{equation*}

A picture that captures this is given by

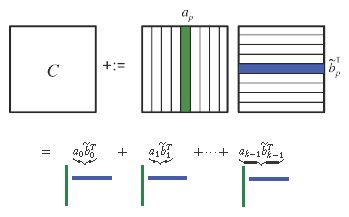
This illustrates how the PJI and PIJ algorithms can be viewed as a loop around rank-1 updates:

\begin{equation*} \begin{array}{l} {\bf for~} p := 0, \ldots , k-1 \\[0.15in] ~~~ \left. \begin{array}{l} {\bf for~} j := 0, \ldots , n-1 \\[0.15in] ~~~ ~~~ \left. \begin{array}{l} {\bf for~} i := 0, \ldots , m-1 \\ ~~~ ~~~ \gamma_{i,j} := \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} \\ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{c_j := \beta_{p,j} a_p + c_j}\\ \mbox{axpy} \end{array} \\[0.2in] ~~~ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{C := a_p \widetilde b_p^T + C}\\ \mbox{rank-1 update} \end{array} \\[0.2in] {\bf end} \end{array} \end{equation*}

and

\begin{equation*} \begin{array}{l} {\bf for~} p := 0, \ldots , k-1 \\[0.15in] ~~~ \left. \begin{array}{l} {\bf for~} i := 0, \ldots , m-1 \\[0.15in] ~~~ ~~~ \left. \begin{array}{l} {\bf for~} j := 0, \ldots , n-1 \\ ~~~ ~~~ \gamma_{i,j} := \alpha_{i,p} \beta_{p,j} + \gamma_{i,j} \\ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{\widetilde c_i^T := \alpha_{i,p} \widetilde b_p^T + \widetilde c_i^T}\\ \mbox{axpy} \end{array} \\[0.2in] ~~~ {\bf end} \end{array} \right\} ~~~ \begin{array}[t]{c} \underbrace{C := a_p \widetilde b_p^T + C}\\ \mbox{rank-1 update} \end{array} \\[0.2in] {\bf end} \end{array} \end{equation*}
login