Unit 1.3.5 Matrix-vector multiplication via axpy operations
¶
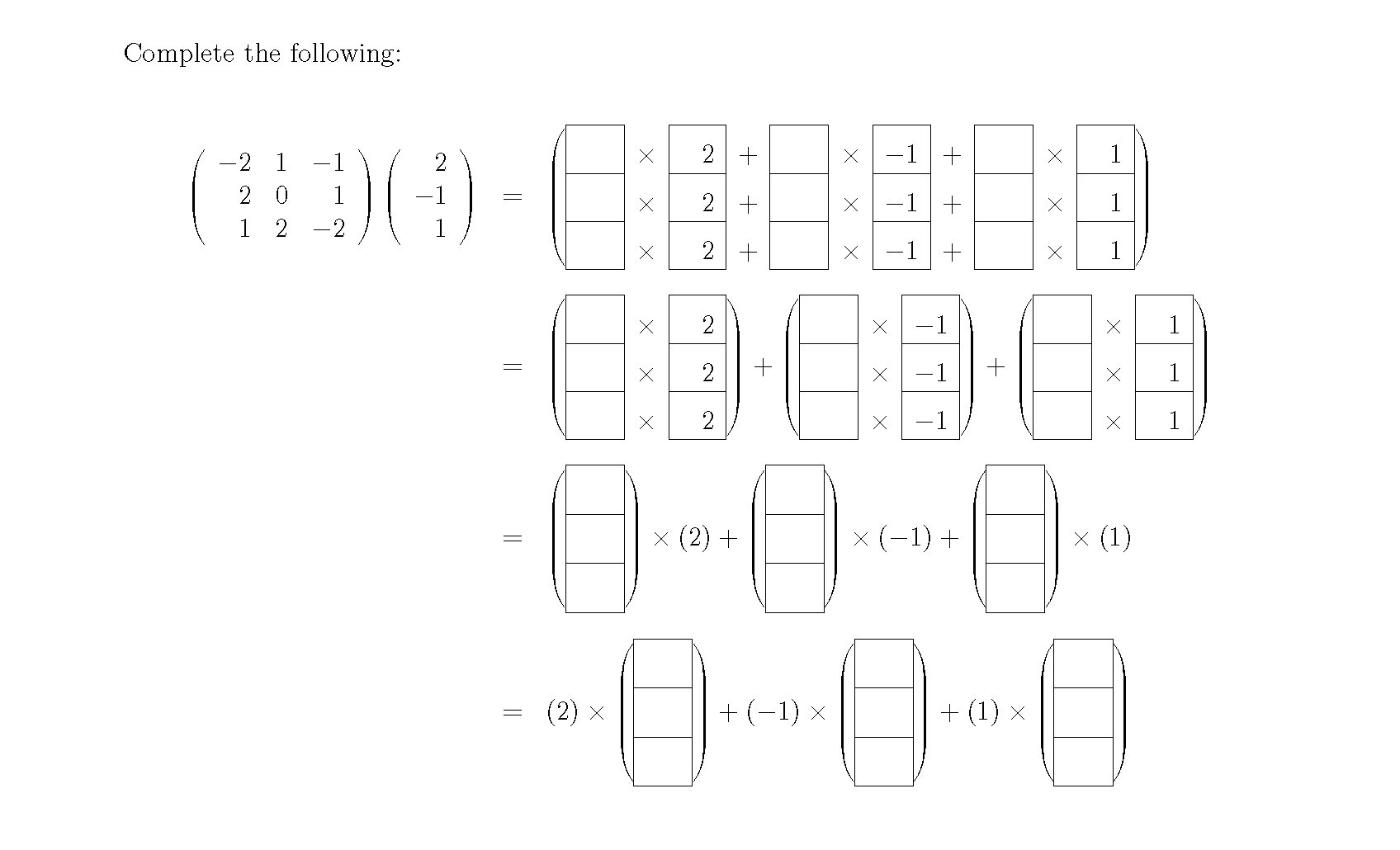
Homework 1.3.5.1 .
Complete
Click here to enlarge.
We now discuss how matrix-vector multiplication can be cast in terms of axpy operations.
VIDEO
We capture the insights from this last exercise: Partition \(m \times n \) matrix \(A \) by columns and \(x \) by individual elements.
\begin{equation*}
\begin{array}{rcl}
y \amp:=\amp
\left( \begin{array}{c | c | c | c}
a_0 \amp a_1 \amp \cdots \amp a_{n-1}
\end{array} \right)
\left( \begin{array}{c}
\chi_0 \\ \hline
\chi_1 \\ \hline
\vdots \\ \hline
\chi_{n-1}
\end{array}
\right) + y \\
\amp=\amp
\chi_0 a_0 + \chi_1 a_1 + \cdots + \chi_{n-1} a_{n-1} + y.
\end{array}
\end{equation*}
If we then expose the individual elements of \(A \) and \(y \) we get
\begin{equation*}
\begin{array}{l}
\left( \begin{array}{c}
\psi_0 \\
\psi_1 \\
\vdots \\
\psi_{m-1}
\end{array}\right) \\
~~~:=
\chi_0
\left( \begin{array}{c}
\alpha_{0,0} \\
\alpha_{1,0} \\
\vdots \\
\alpha_{m-1,0}
\end{array}\right)
+
\chi_1
\left( \begin{array}{c}
\alpha_{0,1} \\
\alpha_{1,1} \\
\vdots \\
\alpha_{m-1,1}
\end{array}\right)
+
\cdots
+
\chi_{n-1}
\left( \begin{array}{c}
\alpha_{0,n-1} \\
\alpha_{1,n-1} \\
\vdots \\
\alpha_{m-1,n-1}
\end{array}\right)
+
\left( \begin{array}{c}
\psi_0 \\
\psi_1 \\
\vdots \\
\psi_{m-1}
\end{array}\right) \\
~~~=
\left( \begin{array}{c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c}
\chi_0 \amp \alpha_{0,0} \amp + \amp
\chi_1 \amp \alpha_{0,1} \amp + \amp \cdots \amp
\chi_{n-1} \amp \alpha_{0,n-1} \amp + \amp \psi_0
\\
\chi_0 \amp \alpha_{1,0} \amp + \amp
\chi_1 \amp \alpha_{1,1} \amp + \amp \cdots \amp
\chi_{n-1} \amp \alpha_{1,n-1} \amp + \amp \psi_1
\\
\amp\amp\amp\amp\amp\vdots\amp\amp\amp \\
\chi_0 \amp \alpha_{m-1,0} \amp + \amp
\chi_1 \amp \alpha_{m-1,1} \amp + \amp \cdots \amp
\chi_{n-1} \amp \alpha_{m-1,n-1} \amp + \amp \psi_{m-1}
\end{array} \right) \\
~~~=
\left( \begin{array}{c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c @{~} c}
\alpha_{0,0} \amp \chi_0 \amp + \amp
\alpha_{0,1} \amp \chi_1 \amp + \amp \cdots \amp
\alpha_{0,n-1} \amp \chi_{n-1} \amp + \amp \psi_0
\\
\alpha_{1,0} \amp \chi_0 \amp + \amp
\alpha_{1,1} \amp \chi_1 \amp + \amp \cdots \amp
\alpha_{1,n-1} \amp \chi_{n-1} \amp + \amp \psi_1
\\
\amp\amp\amp\amp\amp\vdots\amp\amp\amp \\
\alpha_{m-1,0} \amp \chi_0 \amp + \amp
\alpha_{m-1,1} \amp \chi_1 \amp + \amp \cdots \amp
\alpha_{m-1,n-1} \amp \chi_{n-1} \amp + \amp \psi_{m-1}
\end{array} \right).
\end{array}
\end{equation*}
This discussion explains the JI loop for computing \(y := A x + y \text{:}\)
\begin{equation*}
\begin{array}{l}
{\bf for~} j := 0, \ldots , n-1 \\
~~~
\left. \begin{array}{l}
{\bf for~} i := 0, \ldots , m-1 \\
~~~ ~~~ \psi_i := \alpha_{i,j} \chi_{j} + \psi_i \\
{\bf end}
\end{array} \right\} ~~~ y := \chi_j a_j + y \\[0.1in]
{\bf end}
\end{array}
\end{equation*}
What it also demonstrates is how matrix-vector multiplication can be implemented as a sequence of axpy operations.
Homework 1.3.5.2 .
In directory Assignments/Week1/C complete the implementation of matrix-vector multiplication in terms of axpy operations
#define alpha( i,j ) A[ (j)*ldA + i ] // map alpha( i,j ) to array A
#define chi( i ) x[ (i)*incx ] // map chi( i ) to array x
#define psi( i ) y[ (i)*incy ] // map psi( i ) to array y
void Axpy( int, double, double *, int, double *, int );
void MyGemv( int m, int n, double *A, int ldA,
double *x, int incx, double *y, int incy )
{
for ( int j=0; j<n; j++ )
Axpy( , , , , , );
}
in file Assignments/Week1/C/Gemv_J_Axpy.c
make J_Axpy
Remember: you implemented the Axpy routine in the last unit, and we did not test it... So, if you get a wrong answer, the problem may be in that implementation.