Skip to main content

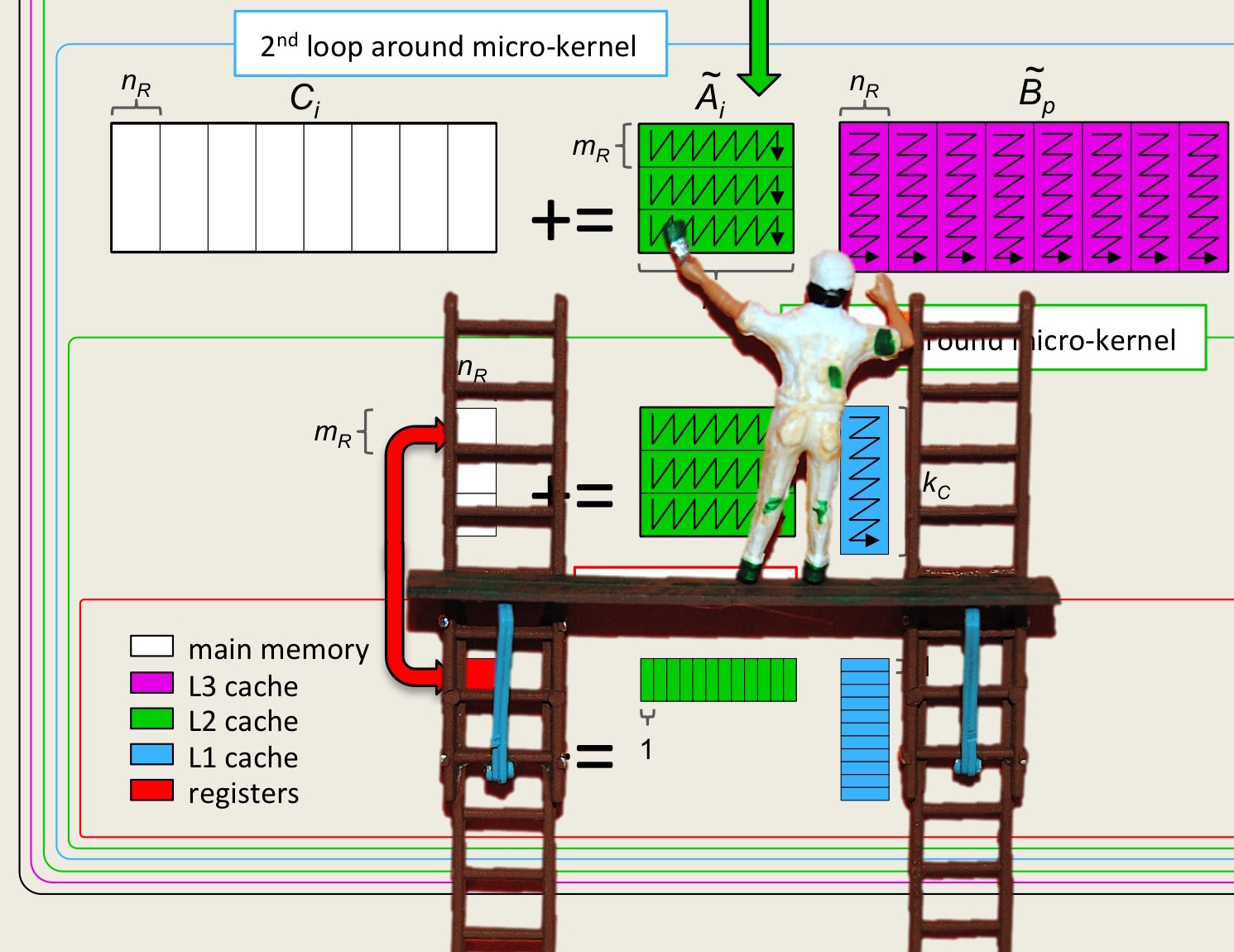
Unit 2.3.4 Combining loops

What we now recognize is that matrices \(A \) and \(B\) need not be partitioned into \(m_R \times k_R \) and \(k_R \times n_R \) submatrices (respectively). Instead, \(A\) can be partitioned into \(m_R \times k\) row panels and \(B\) into \(k \times n_R \) column panels:

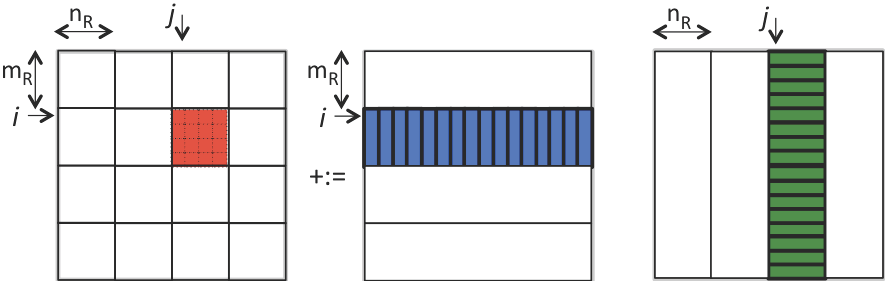
Another way of looking at this is that the inner loop indexed with \(p \) in the blocked algorithm can be combined with the outer loop of the kernel. The entire update of the \(m_R \times n_R \) submatrix of \(C \) can then be pictured as
This is the computation that will later become instrumental in optimizing and will be called the micro-kernel.

Homework 2.3.4.1.

In directory Assignments/Week2/C copy the file Assignments/Week2/C/Gemm_JIP_P_Ger.c into Gemm_JI_P_Ger.c and remove the \(p \) loop from MyGemm. Execute it with 

make JI_P_Ger

and view its performance with Assignments/Week2/C/data/Plot_register_blocking.mlx

Solution

This is the performance on Robert's laptop, with MB=NB=KB=4:

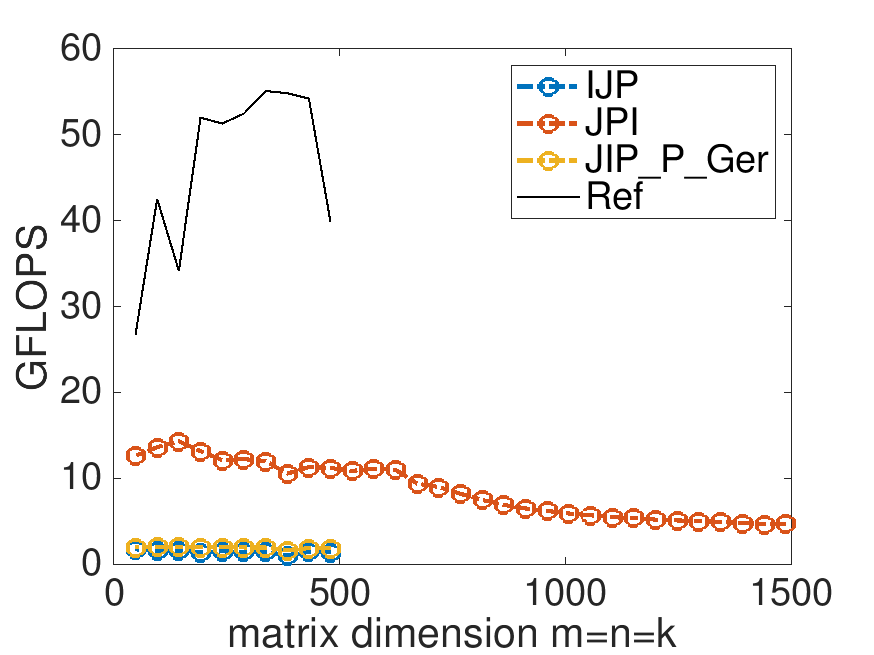
The performance does not really improve, and continues to be pathetic.

Again, it is tempting to start playing with the parameters MB, NB, and KB. However, the point of this exercise is to illustrate the discussion about how the loops indexed with \(p \) can be combined, casting the multiplication with the blocks in terms of a loop around rank-1 updates.

Homework 2.3.4.2.

In detail explain the estimated cost of the implementation in Homework 2.3.4.1.

Solution

Bringing \(A_{i,p} \) one column at a time into registers and \(B_{p,j} \) one row at a time into registers does not change the cost of reading that data. So, the cost of the resulting approach is still estimated as

\begin{equation*} \begin{array}{l} M N K ( 2 m_R n_R k_R ) \gamma_R + \left[ M N ( 2 m_R n_R ) + M N K (m_R k_R + k_R n_R )\right] \beta_{R \leftrightarrow M} \\ ~~~= 2 m n k \gamma_R+ \left[ 2 m n + m n k ( \frac{1}{n_R} + \frac{1}{m_R} ) \right] \beta_{R \leftrightarrow M}. \end{array} \end{equation*}

Here

  • \(2 m n k \gamma_R \) is time spent in useful computation.

  • \(\left[ 2 m n + m n k ( \frac{1}{n_R} + \frac{1}{m_R} ) \right] \beta_{R \leftrightarrow M} \) is time spent moving data around, which is overhead.

The important insight is that now only the \(m_R \times n_R \) micro-tile of \(C \text{,}\) one small column \(A \) of size \(m_R \) one small row of \(B\) of size \(n_R \) need to be stored in registers. In other words, \(m_R \times n_R + m_R + n_R \) doubles are stored in registers at any one time.

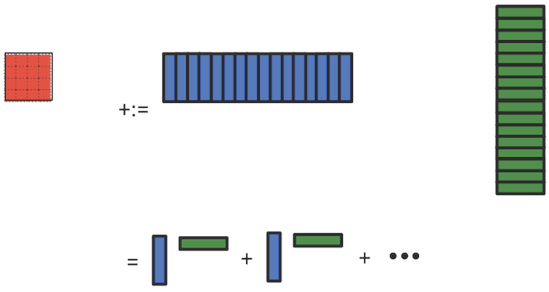
One can go one step further: Each individual rank-1 update can be implemented as a sequence of axpy operations:

\begin{equation*} \begin{array}{l} \left( \begin{array}{c| c |c | c} \gamma_{0,0} \amp \gamma_{0,1} \amp \gamma_{0,2} \amp \gamma_{0,3} \\ \gamma_{1,0} \amp \gamma_{1,1} \amp \gamma_{1,2} \amp \gamma_{1,3} \\ \gamma_{2,0} \amp \gamma_{2,1} \amp \gamma_{2,2} \amp \gamma_{2,3} \\ \gamma_{3,0} \amp \gamma_{3,1} \amp \gamma_{3,2} \amp \gamma_{3,3} \end{array} \right) +:= \left( \begin{array}{c} \alpha_{0,p} \\ \alpha_{1,p} \\ \alpha_{2,p} \\ \alpha_{3,p} \end{array} \right) \left( \begin{array}{c | c | c | c} \beta_{p,0} \amp \beta_{p,1} \amp \beta_{p,2} \amp \beta_{p,3} \end{array} \right) \\ ~~~= \left( \begin{array}{c | c | c | c} \beta_{p,0} \left( \begin{array}{c} \alpha_{0,p} \\ \alpha_{1,p} \\ \alpha_{2,p} \\ \alpha_{3,p} \end{array} \right) \amp \beta_{p,1} \left( \begin{array}{c} \alpha_{0,p} \\ \alpha_{1,p} \\ \alpha_{2,p} \\ \alpha_{3,p} \end{array} \right) \amp \beta_{p,2} \left( \begin{array}{c} \alpha_{0,p} \\ \alpha_{1,p} \\ \alpha_{2,p} \\ \alpha_{3,p} \end{array} \right) \amp \beta_{p,3} \left( \begin{array}{c} \alpha_{0,p} \\ \alpha_{1,p} \\ \alpha_{2,p} \\ \alpha_{3,p} \end{array} \right) \end{array} \right) . \end{array} \end{equation*}

Here we note that if the block of \(C \) is updated one column at a time, the corresponding element of \(B \text{,}\) \(\beta_{p,j} \) in our discussion, is not reused and hence only one register is needed for the elements of \(B \text{.}\) Thus, when \(m_R = n_R = 4 \text{,}\) we have gone from storing \(48 \) doubles in registers to \(24 \) and finally to only \(21 \) doubles.. More generally, we have gone from \(m_R n_R + m_R k_R + k_R n_R \) to \(m_R n_R + m_R + n_R \) to

\begin{equation*} m_R n_R + m_R + 1 \end{equation*}

doubles.

Obviously, one could have gone further yet, and only store one element \(\alpha_{i,p} \) at a time. However, in that case one would have to reload such elements multiple times, which would adversely affect overhead.

login