Unit 3.5.1 Goto's algorithm and BLIS
¶The overall approach described in Week 2 and Week 3 was first suggested by Kazushige Goto and published in
[9] Kazushige Goto and Robert van de Geijn, On reducing TLB misses in matrix multiplication, Technical Report TR02-55, Department of Computer Sciences, UT-Austin, Nov. 2002.
[10] Kazushige Goto and Robert van de Geijn, Anatomy of High-Performance Matrix Multiplication, ACM Transactions on Mathematical Software, Vol. 34, No. 3: Article 12, May 2008.
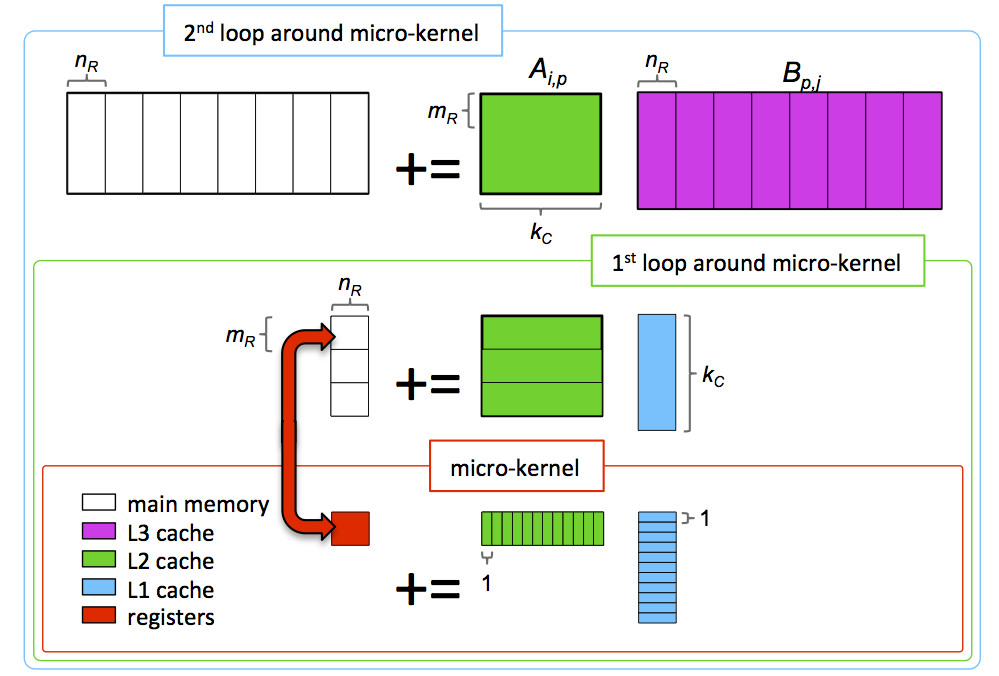
We refer to it as Goto's algorithm or the GotoBLAS algorithm (since he incorporated it in his implementation of the BLAS by the name GotoBLAS). His innovations included staging the loops so that a block of \(A \) remains in the L2 cache. He assembly-coded all the computation performed by the two loops around the micro-kernel
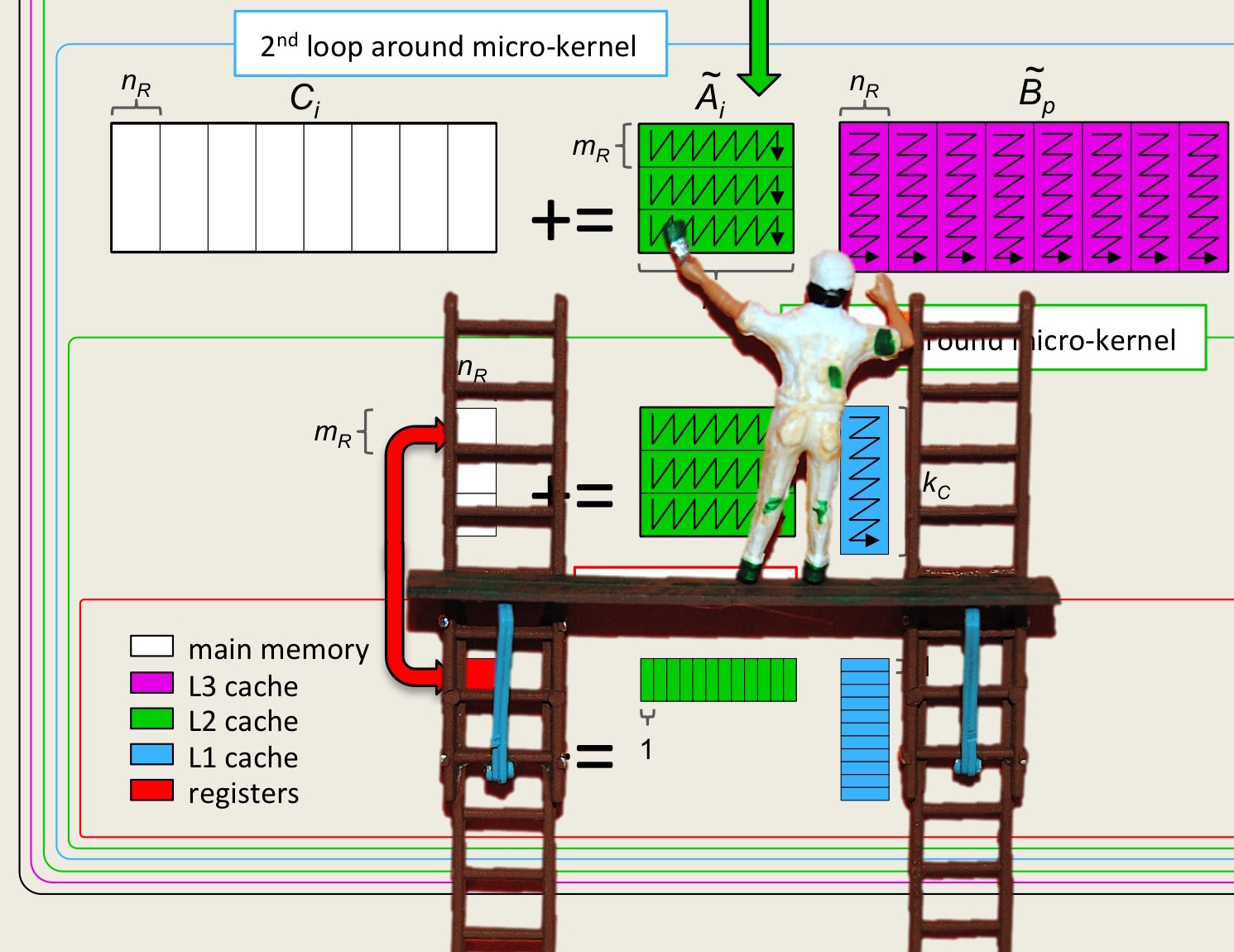
The very specific packing by micro-panels that we discuss in this week was also incorporated in Goto's implementations but the idea should be attributed to Greg Henry.
The BLIS library refactored Goto's algorithm into the five loops around the micro-kernel with which you are now very familiar, as described in a sequence of papers:
[32] Field G. Van Zee and Robert A. van de Geijn, BLIS: A Framework for Rapidly Instantiating BLAS Functionality, ACM Journal on Mathematical Software, Vol. 41, No. 3, June 2015.
[31] Field G. Van Zee, Tyler Smith, Francisco D. Igual, Mikhail Smelyanskiy, Xianyi Zhang, Michael Kistler, Vernon Austel, John Gunnels, Tze Meng Low, Bryan Marker, Lee Killough, and Robert A. van de Geijn, The BLIS Framework: Experiments in Portability, ACM Journal on Mathematical Software, Vol. 42, No. 2, June 2016.
[27] Field G. Van Zee and Tyler M. Smith, Implementing High-performance Complex Matrix Multiplication via the 3M and 4M Methods, ACM Transactions on Mathematical Software, Vol. 44, No. 1, pp. 7:1-7:36, July 2017.
[30] Field G. Van Zee, Implementing High-Performance Complex Matrix Multiplication via the 1m Method, ACM Journal on Mathematical Software, in review.
While Goto already generalized his approach to accommodate a large set of special cases of matrix-matrix multiplication, known as the level-3 BLAS [5], as described in
[11] Kazushige Goto and Robert van de Geijn, High-performance implementation of the level-3 BLAS, ACM Transactions on Mathematical Software, Vol. 35, No. 1: Article 4, July 2008.
His implementations required a considerable amount of assembly code to be written for each of these special cases. The refactoring of matrix-matrix multiplication in BLIS allows the micro-kernel to be reused across these special cases [32], thus greatly reducing the effort required to implement all of this functionality, at the expense of a moderate reduction in performance.