Skip to main content

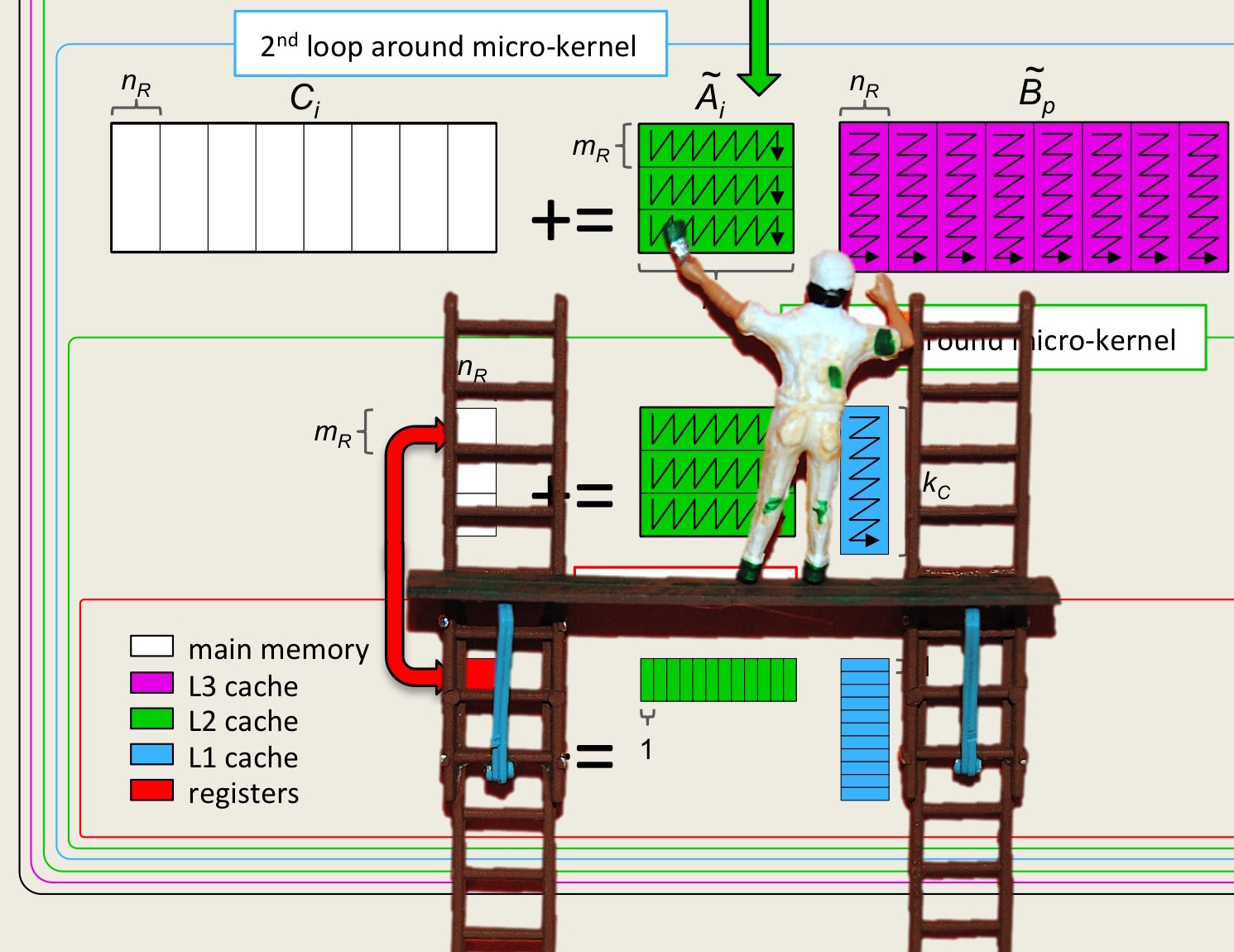
Unit 3.3.3 Implementation: packing row panel \(B_{p,j} \)

We briefly discuss the packing of the row panel \(B_{p,j} \) into \(\widetilde B_{p,j} \text{:}\)

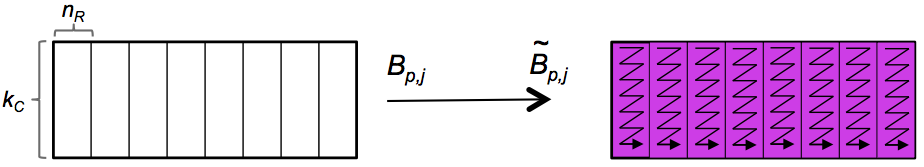
We break the implementation, in Assignments/Week3/C/PackB.c, down into two routines. The first loops over all the panels that need to be packed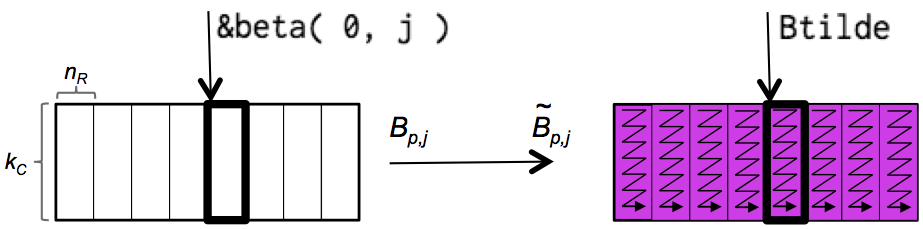

as illustrated in Figure 3.3.2.

void PackPanelB_KCxNC( int k, int n, double *B, int ldB, double *Btilde )
/* Pack a k x n panel of B in to a KC x NC buffer.
.  
   The block is copied into Btilde a micro-panel at a time. */
{
  for ( int j=0; j<n; j+= NR ){
    int jb = min( NR, n-j );
    
    PackMicro-PanelB_KCxNR( k, jb, &beta( 0, j ), ldB, Btilde );
    Btilde += k * jb;
  }
}

Figure 3.3.2. A reference implementation for packing \(B_{p,j} \text{.}\)

That routine then calls a routine that packs the panel

Given in Figure 3.3.3.

void PackMicroPanelB_KCxNR( int k, int n, double *B, int ldB,
	    double *Btilde )
/* Pack a micro-panel of B into buffer pointed to by Btilde.
   This is an unoptimized implementation for general KC and NR.
   k is assumed to be less then or equal to KC.
   n is assumed to be less then or equal to NR.  */
{
  /* March through B in row-major order, packing into Btilde. */
  if ( n == NR ) {
    /* Full column width micro-panel.*/
    for ( int p=0; p<k; p++ )
      for ( int j=0; j<NR; j++ )
        *Btilde++ = beta( p, j );
  }
  else {
    /* Not a full row size micro-panel. We pad with zeroes.
     To be added */
  }
}

Figure 3.3.3. A reference implementation for packing a micro-panel of \(B_{p,j} \text{.}\)
Remark 3.3.4.

We emphasize that this is a “quick and dirty” implementation. It is meant to be used for matrices that are sized to be nice multiples of the various blocking parameters. The goal of this course is to study how to implement matrix-matrix multiplication for matrices that are nice multiples of these blocking sizes. Once one fully understands how to optimize that case, one can start from scratch and design an implementation that works for all matrix sizes. Alternatively, upon completing this week one understands the issues well enough to be able to study a high-quality, open source implementation like the one in our BLIS framework [3].

login