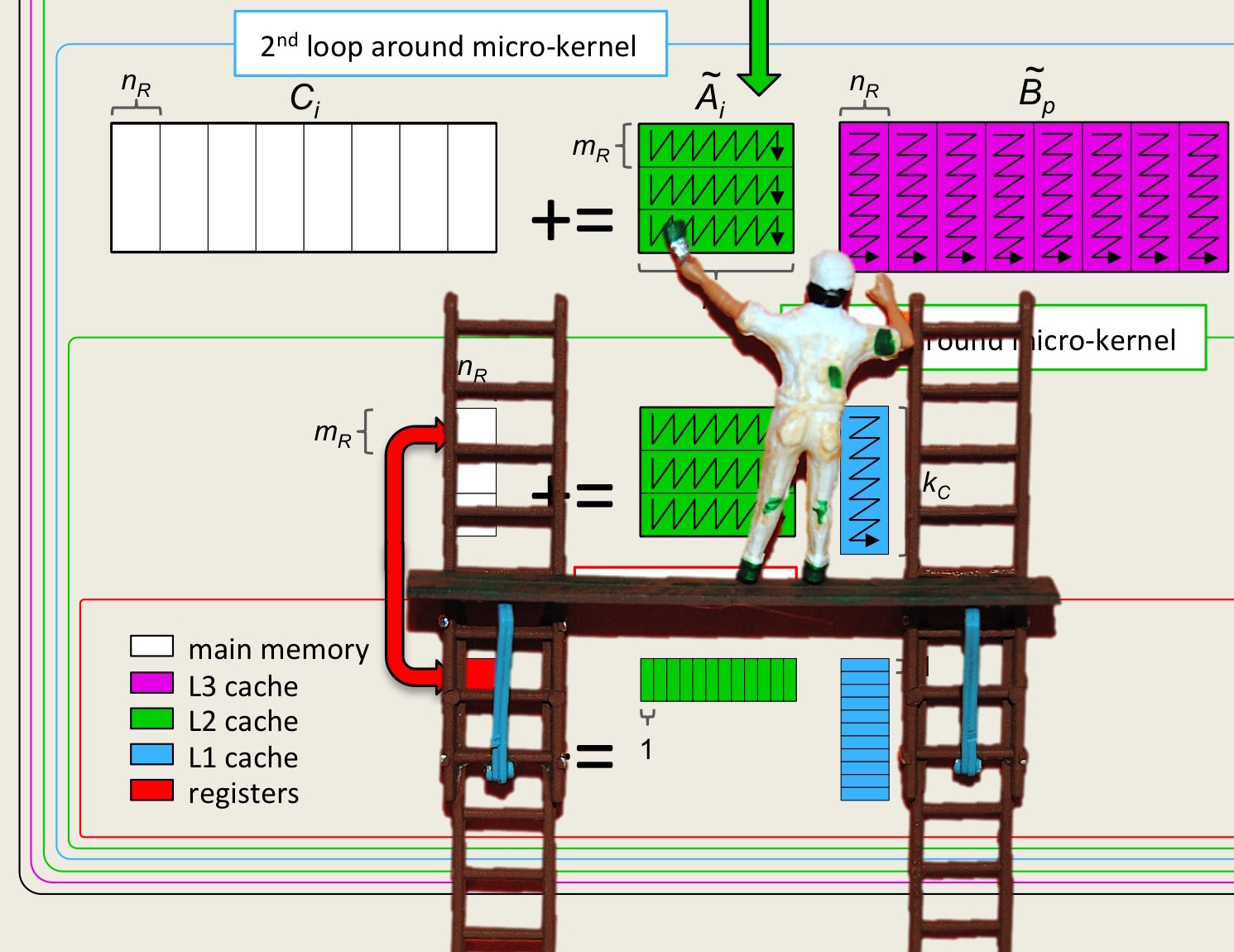
Unit 3.3.1 Stride matters
¶
Homework 3.3.1.1.
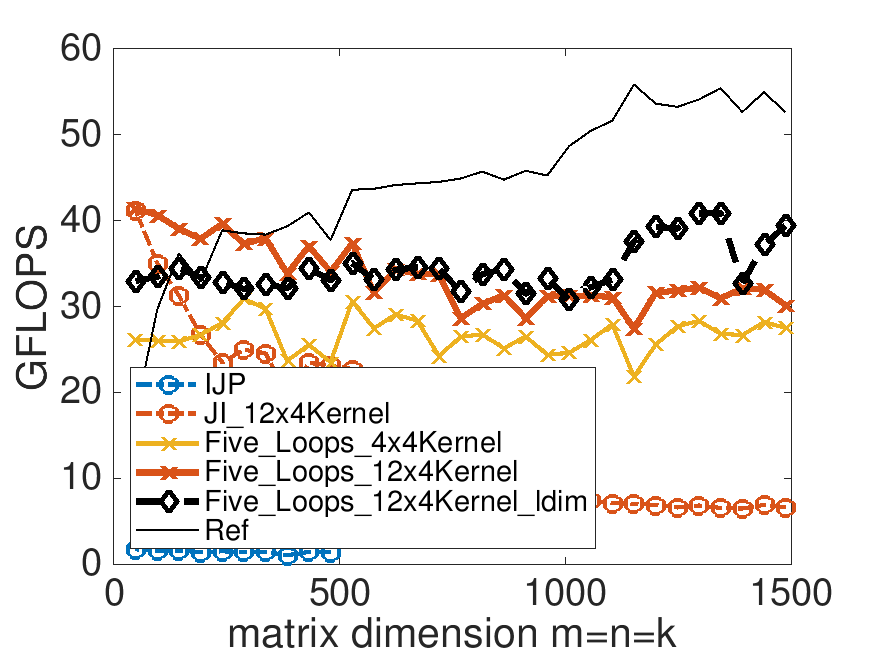
One would think that once one introduces blocking, the higher performance attained for small matrix sizes will be maintained as the problem size increases. This is not what you observed: there is still a decrease in performance. To investigate what is going on, copy the driver routine in Assignments/Week3/C/driver.c into driver_ldim.c and in that new file change the line
ldA = ldB = ldC = size;to
ldA = ldB = ldC = last;This sets the leading dimension of matrices \(A\text{,}\) \(B \text{,}\) and \(C \) to the largest problem size to be tested, for all experiments. Collect performance data by executing
make Five_Loops_12x4Kernel_ldimin that directory. The resulting performance can be viewed with Live Script
Assignments/Week3/C/data/Plot_Five_Loops.mlx.
What is going on here? Modern processors incorporate a mechanism known as "hardware prefetching" that speculatively preloads data into caches based on observed access patterns so that this loading is hopefully overlapped with computation. Processors also organize memory in terms of pages, for reasons that have to do with virtual memory, details of which go beyond the scope of this course. For our purposes, a page is a contiguous block of memory of 4 Kbytes (4096 bytes or 512 doubles). Prefetching only occurs within a page. Since the leading dimension is now large, when the computation moves from column to column in a matrix data is not prefetched.
The bottom line: early in the course we discussed that marching contiguously through memory is a good thing. While we claim that we do block for the caches, in practice the data is typically not contiguously stored and hence we can't really control how the data is brought into caches, where it exists at a particular time in the computation, and whether prefetching is activated. Next, we fix this through packing of data at strategic places in the nested loops.
Learn more:
Memory page:
https://en.wikipedia.org/wiki/Page_(computer_memory).Cache prefetching:
https://en.wikipedia.org/wiki/Cache_prefetching.