On this tour you will learn a little about what ACL2 is for rather than how ACL2 works. At the bottom of the ``page'' (which may extend beyond the end of your screen) there is a small ``flying tour'' icon. Click on it to go to the next page of the tour.
The tour visits the following topics sequentially.
The Flight Plan
* This Documentation
* What is ACL2?
* Mathematical Logic
* Mechanical Theorem Proving
* Mathematical Models in General
* Mathematical Models of Computing Machines
Formalizing Models
Running Models
Symbolic Execution of Models
Proving Theorems about Models
* Requirements of ACL2
The User's Skills
Training
Host System
We intend the tour to take about 10 minutes of your time. Some pages on the tour contain pointers to other documents. You need not follow these pointers to stay on the tour.
Below we show the first target term, extracted from the current conjecture. Below it we show the associativity rule.
The variables of the rewrite rule are instantiated so that the left-hand side of the rule matches the target:
variable term from target
a x1
b x2
c (app x3 x4)
Then the target is replaced by the instantiated right-hand side of the rule.
Sometimes rules have hypotheses. To make a long story short, if the rule has hypotheses, then after matching the left-hand side, the rewriter instantiates the hypotheses and rewrites them recursively. This is called backchaining. If they all rewrite to true, then the target is replaced as above.
For more details on how the ACL2 rewriter works, see Boyer and Moore's
book A Computational Logic, Academic Press, 1979.
This warning sign, which usually appears as ``
'',
indicates that the link it marks takes you into ACL2's online
documentation.
The documentation is a vast graph of documented topics intended to
help the user of ACL2 rather than the potential user. If
you are exploring ACL2's home page to learn about the system,
perhaps you should go back rather than follow the link marked with
this sign. But you are welcome to explore the online documentation
as well. Good luck.
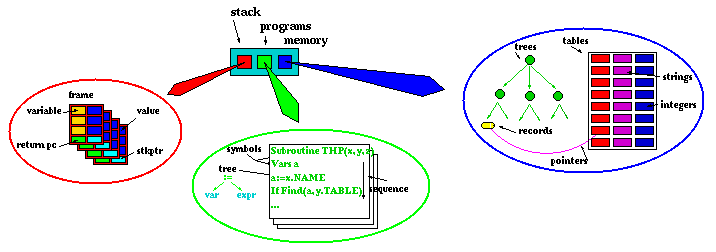
Observe that the states in typical models talk about
booleans integers vectors records caches bits symbols arrays stacks files characters strings sequences tables directories
These objects are discrete rather than continuous; furthermore they are built incrementally or inductively by repeatedly using primitive operations to put together smaller peices.
The functions we need to manipulate these objects do things like concatenate, reverse, sort, search, count, etc.
On this tour you will learn a little more about the ACL2 logic, the theorem prover, and the user interface.
This time we will stick with really simple things, such as the associativity of list concatenation.
We assume you have taken the Flying Tour but that you did not necessarily follow all the ``off-tour'' links. So this tour may revisit some pages you've seen. Just click on the Walking Tour icon at the bottom of each page.
On this tour you will see many more links marked . We would
like to discourage you from following these links right
now. However we encourage you to note them. Basically, the
sign here illustrates the documentation and introduces you to
its main entry points. Once you have started to use ACL2 you can
take the Walking Tour again but pursue more of the indicated links.
ACL2 accepts 256 distinct characters, which are the characters
obtained by applying the function code-char to each
integer from 0 to 255. Among these, Common Lisp designates certain
ones as *standard-characters*, namely those of the form
(code-char n) where n is from 33 to 126, together with
#\Newline and #\Space. The actual standard characters may
be viewed by evaluating the constant expression
*standard-chars*.
The standard character constants are written by writing a hash mark followed by a backslash (#\) followed by the character.
The function characterp recognizes characters. For more
details, See characters .
The function cons creates an ordered pair. Car
and cdr return the first and second components,
respectively, of an ordered pair. The function consp
recognizes ordered pairs.
Ordered pairs are used to represent lists and trees. See any Common Lisp
documentation for a discussion of how list constants are written and for
the many list processing functions available. Also, see programming
where we list all the ACL2 primitive functions.
Here are some examples of list constants to suggest their syntax.
'(a . b) ; a pair whose car is 'a and cdr is 'b
'(a . nil) ; a pair whose car is 'a and cdr is nil
'(a) ; another way to write the same thing
'(a b) ; a pair whose car is 'a and cdr is '(b)
'(a b c) ; a pair whose car is 'a and cdr is '(b c)
; i.e., a list of three symbols, a, b, and c.
'((a . 1) (b . 2)) ; a list of two pairs
It is useful to distinguish ``proper'' conses from ``improper'' ones,
the former being those cons trees whose right-most branch terminates with
nil. A ``true list'' (see true-listp ) is either nil
or a proper cons. (A b c . 7) is an improper cons and hence not a
true list.
Strings of ACL2 characters are written as sequences of characters delimited by ``double quotation marks'' ("). To put such a character in a string, escape it by preceding it with a backslash.
The function stringp recognizes strings and char
will fetch the nth character of a string. There are many
other primitives for handling strings, such as string< for
comparing two strings lexicographically. We suggest you
See programming where we list all of the primitive ACL2
functions. Alternatively, see any Common Lisp language
documentation.
Common Lisp's symbols are a data type representing words. They are
frequently regarded as atomic objects in the sense that they are not
frequently broken down into their constituents. Often the only
important properties of symbols is that they are not numbers,
characters, strings, or lists and that two symbols are not equal if
they look different (!). Examples of symbols include PLUS and
SMITH::ABC. All function and variable names in ACL2 are symbols.
When symbols are used as constants they must be quoted, as in
'PLUS.
The symbol T is commonly used as the Boolean ``true.'' The
symbol NIL is commonly used both as the Boolean ``false'' and as
the ``empty list.'' Despite sometimes being called the ``empty
list'' NIL is a symbol not an ``empty cons.'' Unlike other
symbols, T and NIL may be used as constants without quoting
them.
Usually, symbols are written as sequences of alphanumeric characters
other than those denoting numbers. Thus, A12, +1A and 1+
are symbols but +12 is a number. Roughly speaking, when symbols
are read lower case characters are converted to upper case, so we
frequently do not distinguish ABC from Abc or abc.
Click here for information about case conversion
when symbols are read. However, any character can be used in a
symbol, but some characters must be ``escaped'' to allow the Lisp
reader to parse the sequence as a symbol. For example, |Abc| is
a symbol whose first character is capitalized and whose remaining
characters are in lower case. |An odd duck| is a symbol
containing two #\Space characters. See any Common Lisp documentation
for the syntactic rules for symbols.
Technically, a symbol is a special kind of pair consisting of a
package name (which is a string) and a symbol name (which is also a
string). (See symbol-package-name and see symbol-name
.) The symbol SMITH::ABC is said to be in package "SMITH"
and to have the symbol name "ABC". The symbol ABC in package
"SMITH" is generally not equal to the symbol ABC in package
"JONES". However, it is possible to ``import'' symbols from one
package into another one, but in ACL2 this can only be done when the
package is created. (See defpkg .) If the
current-package is "SMITH" then SMITH::ABC may be
more briefly written as just ABC. Intern ``creates''
a symbol of a given name in a given package.
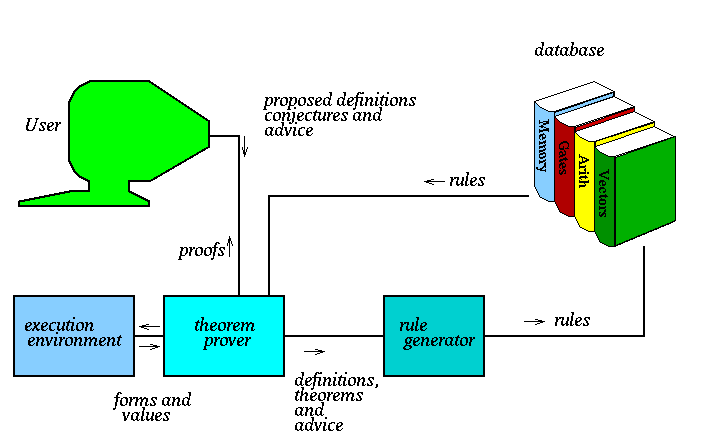
The user interacts with the theorem prover by giving it definitions,
theorems and advice (e.g., ``use this lemma.''), often in the form
of books books .
The theorem prover uses the rules in the library of books the user has selected.
The theorem prover prints its proof attempts to the user.
When a theorem is proved it is converted to a rule under the control
of the user's rule-classes .
The informed user can make ACL2 do amazing things.
The ACL2 theorem prover finds proofs in the ACL2 logic. It can be automatic. But most often the user must help it.
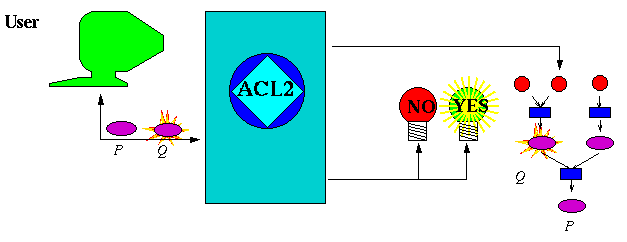
The user usually guides ACL2 by suggesting that it first prove key lemmas. Lemmas are just theorems used in the proofs of other theorems.
Click here to continue.
Theorems, lemmas, definitions, and advice of various sorts can be
stored in books .
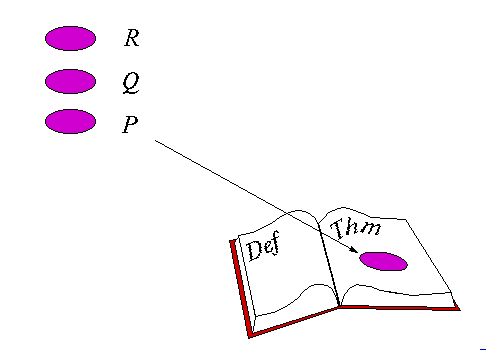
When a theorem or definition is stored in a book, the user can specify how it should be used in the future. When viewed this way, theorems and definitions are thought of as rules.
The ACL2 theorem prover is rule driven. The rules are obtained from books.
Click here to continue.
The example
ACL2 !>(app '(a b c) 27) (A B C . 27)illustrates the fact that ACL2's logic is untyped (click here for a brief discussion of the typed versus untyped nature of the logic).
The definition of app makes no restriction of the arguments to lists.
The definition says that if the first argument satisfies endp
then return the second argument. In this example, when app has recursed
three times down the cdr of its first argument, '(a b c), it
reaches the final nil, which satisfies endp, and so 27 is returned.
It is naturally consed into the emerging list as the function returns from
successive recursive calls (since cons does not require its arguments
to be lists, either). The result is an ``improper'' list, (a b c . 27).
You can think of (app x y) as building a binary tree by replacing
the right-most tip of the tree x with the tree y.
ACL2 is used to construct mathematical models of computer hardware and software (i.e., ``digital systems'').
A mathematical model is a set of mathematical formulas used to predict the behavior of some artifact.
The use of mathematical models allows faster and cheaper delivery of better systems.
Models need not be complete or perfectly accurate to be useful to the trained engineer.
Click here for more discussion of these assertions in an engineering context.
t is a ``symbol'' and 3 is an ``integer.''
Roughly speaking the objects of ACL2 can be partitioned into the
following types:
Numbers3, -22/7, #c(3 5/2)Characters#\A, #\a, #\SpaceStrings"This is a string."Symbols'abc, 'smith::abcConses (or Ordered Pairs)'((a . 1) (b . 2))
When proving theorems it is important to know the types of object
returned by a term. ACL2 uses a complicated heuristic algorithm,
called type-set , to determine what types of objects a
term may produce. The user can more or less program the
type-set algorithm by proving type-prescription
rules.
ACL2 is an ``untyped'' logic in the sense that the syntax is not
typed: It is legal to apply a function symbol of n arguments to any
n terms, regardless of the types of the argument terms. Thus, it is
permitted to write such odd expressions as (+ t 3) which sums the
symbol t and the integer 3. Common Lisp does not prohibit such
expressions. We like untyped languages because they are simple to
describe, though proving theorems about them can be awkward because,
unless one is careful in the way one defines or states things,
unusual cases (like (+ t 3)) can arise.
To make theorem proving easier in ACL2, the axioms actually define a
value for such terms. The value of (+ t 3) is 3; under the ACL2
axioms, non-numeric arguments to + are treated as though they
were 0.
You might immediately wonder about our claim that ACL2 is Common
Lisp, since (+ t 3) is ``an error'' (and will sometimes even
``signal an error'') in Common Lisp. It is to handle this problem that
ACL2 has guards. We will discuss guards later in the Walking Tour.
However, many new users simply ignore the issue of guards entirely.
You should now return to the Walking Tour.
The ACL2 Home Page is integrated into the ACL2 online documentation. Over 1.5 megabytes of text is available here.
The vast majority of the text
is user-level documentation. For example, to find out about rewrite
rules you could click on the word ``rewrite .''
But before you do that remember that you must then use your browser's
back commands to come back here.
The tiny warning signs mark pointers that lead out of the
introductory-level material and into the user documentation. If you are
taking the Flying Tour, we advise you to avoid following such pointers the
first time; it is easy to get lost in the full documentation unless
you are pursuing the answer to a specific question. If you do wander down
these other paths, remember you can back out to a page containing the
Flying Tour icon to resume the tour.
At the end of the tour you will have a chance to return to The Flight Plan where you can revisit the main stops of the Flying Tour and explore the alternative paths more fully.
Finally, every page contains two icons at the bottom. The ACL2 icon leads you back to the ACL2 Home Page. The Index icon allows you to browse an alphabetical listing of all the topics in ACL2's online documentation.
APP
must have several properties to be admitted to the logic as a new
axiom
The key property a recursive definition must have is that the recursion terminate. This, along with some syntactic criteria, insures us that there exists a function satisfying the definition.
Termination must be proved before the definition is admitted. This is done in general by finding a measure of the arguments of the function and a well-founded relation such that the arguments ``get smaller'' every time a recursive branch is taken.
For app the measure is the ``size'' of the first argument, x,
as determined by the primitive function acl2-count . The
well-founded relation used in this example is e0-ordinalp
, which is the standard ordering on the ordinals less than
``epsilon naught.'' These particular choices for app were made
``automatically'' by ACL2. But they are in fact determined by
various ``default'' settings. The user of ACL2 can change the
defaults or specify a ``hint'' to the defun command to
specify the measure and relation.
You should now return to the Walking Tour.
ACL2 !>'' is the ACL2 prompt.
The prompt tells the user that an ACL2 command is expected. In
addition, the prompt tells us a little about the current state of
the ACL2 command interpreter. We explain the prompt briefly below.
But first we talk about the command interpreter.
An ACL2 command is generally a Lisp expression to be evaluated.
There are some unusual commands (such as :q for quitting
ACL2) which cause other behavior. But most commands are read,
evaluated, and then have their results printed. Thus, we call the
command interpreter a ``read-eval-print loop.'' The ACL2 command
interpreter is named LD (after Lisp's ``load'').
A command like (defun app (x y) ...) causes ACL2 to evaluate the
defun function on app, (x y) and .... When
that command is evaluated it prints some information to the terminal
explaining the processing of the proposed definition. It returns
the symbol APP as its value, which is printed by the command
interpreter. (Actually, defun is not a function but a macro
which expands to a form that involves state , a necessary
precondition to printing output to the terminal and to ``changing''
the set of axioms. But we do not discuss this further here.)
The defun command is an example of a special kind of command
called an ``event.'' Events are those commands that
change the ``logical world'' by adding such things as axioms or
theorems to ACL2's data base. See world . But not
every command is an event command.
A command like (app '(1 2 3) '(4 5 6 7)) is an example of a non-event. It is processed the same general way: the function app is applied to the indicated arguments and the result is printed. The function app does not print anything and does not change the ``world.''
A third kind of command are those that display information about the
current logical world or that ``backup'' to previous versions of the
world. Such commands are called ``history'' commands.
What does the ACL2 prompt tell us about the read-eval-print loop?
The prompt ``ACL2 !>'' tells us that the command will be read
with current-package set to "ACL2", that guard checking
(see set-guard-checking ) is on (``!''), and that we are at
the top-level (there is only one ``>'').
For more about the prompt, see default-print-prompt .
You should now return to the Walking Tour.
Consider the binary trees x and y below.
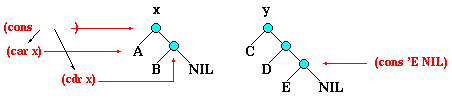
In Lisp, x is written as the list '(A B) or, equivalently, as
'(A B . NIL). Similarly, y may be written '(C D E).
Suppose we wish to replace the right-most tip of x
by the entire tree y. This is denoted (app x y), where app
stands for ``append''.
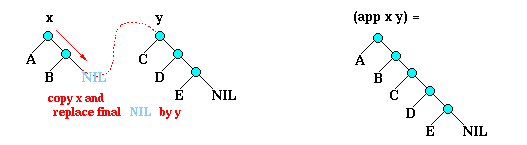
We can define app with:
(defun app (x y) ; Concatenate x and y.
(declare (type (satisfies true-listp) x)); We expect x to end in NIL.
(cond ((endp x) y) ; If x is empty, return y.
(t (cons (car x) ; Else, copy first node
(app (cdr x) y))))) ; and recur into next.
If you defined this function in some Common Lisp, then to run
app on the x and y above you could then type
(app '(A B) '(C D E))and Common Lisp will print the result
(A B C D E).
app function discussed
in the Common Lisp page, except we will omit
for the moment the declare form, which in ACL2 is called a guard.
We will deal with guards later. Here is the definition again
(defun app (x y)
(cond ((endp x) y)
(t (cons (car x)
(app (cdr x) y)))))
The next few stops along the Walking Tour will show you
* how to use the ACL2 documentation, * what happens when the above definition is submitted to ACL2, * what happens when you evaluate calls ofAlong the way we will talk about the definitional principle, types, the ACL2 read-eval-print loop, and how the theorem prover works.app, * what one simple theorem aboutapplooks like, * how ACL2 proves the theorem, and * how that theorem can be used in another proof.
When we complete this part of the tour we will introduce the notion of guards and revisit several of the topics above in that context.
To analyze a model you must be able to reason about the operations and relations involved. Perhaps, for example, some aspect of the model depends upon the fact that the concatenation operation is associative.
In any Common Lisp you can confirm that
(app '(A B) (app '(C D) '(E F)))and
(app (app '(A B) '(C D)) '(E F)))both evaluate to the same thing,
(A B C D E F).
But what distinguishes ACL2 (the logic) from applicative Common Lisp (the
language) is that in ACL2 you can prove that the concatenation
function app is associative when its arguments are true-lists,
whereas in Common Lisp all you can do is test that proposition.
That is, in ACL2 it makes sense to say that the following formula is a ``theorem.''
Theorem Associativity of App
(implies (and (true-listp a)
(true-listp b))
(equal (app (app a b) c)
(app a (app b c))))
Theorems about the properties of models are proved by symbolically
manipulating the operations and relations involved. If the
concatenation of sequences is involved in your model, then you may
well need the theorem above in order to that your model has some
particular property.
The logic of ACL2 is based on Common Lisp.
Common Lisp is the standard list processing programming language. It is documented in: Guy L. Steele, Common Lisp The Language, Digital Press, 12 Crosby Drive, Bedford, MA 01730, 1990.
ACL2 formalizes only a subset of Common Lisp. It includes such
familiar Lisp functions as cons, car and cdr for creating
and manipulating list structures, various arithmetic primitives such
as +, *, expt and <=, and intern and symbol-name for
creating and manipulating symbols. Control primitives include
cond, case and if, as well as function call, including
recursion. New functions are defined with defun and macros with
defmacro. See programming for a list of the Common
Lisp primitives supported by ACL2.
ACL2 is a very small subset of full Common Lisp. ACL2 does not
include the Common Lisp Object System (CLOS), higher order
functions, circular structures, and other aspects of Common Lisp
that are non-applicative. Roughly speaking, a language is
applicative if it follows the rules of function application. For
example, f(x) must be equal to f(x), which means, among other
things, that the value of f must not be affected by ``global
variables'' and the object x must not change over time.
Click here for a simple example of Common Lisp.
In ACL2 we have adopted Common Lisp as the basis of our modeling language.
If you have already read our brief note on Common Lisp and recall
the example of app, please proceed. Otherwise
click here for an exceedingly brief introduction to
Common Lisp and then come back here.
In Common Lisp it is very easy to write systems of formulas that manipulate discrete, inductively constructed data objects. In building a model you might need to formalize the notion of sequences and define such operations as concatenation, length, whether one is a permutation of the other, etc. It is easy to do this in Common Lisp. Furthermore, if you have a Common Lisp ``theory of sequences'' you can run the operations and relations you define. That is, you can execute the functions on concrete data to see what results your formulas produce.
If you define the function app as shown above and then type
(app '(A B) '(C D E))in any Common Lisp, the answer will be computed and will be
(A B C D E).The executable nature of Common Lisp and thus of ACL2 is very handy when producing models.
But executability is not enough for a modeling language because the purpose of models is to permit analysis.
Click here to continue.
To type a symbol containing lower case characters you can enclose the
symbol in vertical bars, as in |AbC| or you can put a ``backslash''
before each lower case character you wish to preserve, as in A\bC.
|AbC| and A\bC are two different ways of writing the same
symbol (just like 4/2 and 1/2 are two different ways of writing the
same rational). The symbol has three characters in its name, the
middle one of which is a lower case b.
After producing a model, it must be corroborated against reality. The Falling Body Model has been corroborated by a vast number of experiments in which the time and distance were measured and compared according to the formula. In general all models must be corroborated by experiment.
The Falling Body Model can be derived from deeper models, namely Newton's laws of motion and the assertion that, over the limited distances concerned, graviation exerts a constant acceleration on the object. When the model in question can be derived from other models, it is the other models that are being corroborated by our experiments.
Because nature is not formal, we cannot prove that our models of it are correct. All we can do is test our models against nature's behavior.
Such testing often exposes restrictions on the applicability of our models. For example, the Falling Body Model is inaccurate if air resistance is significant. Thus, we learn not to use that model to predict how long it takes a feather to fall from a 200 foot tower in the earth's atmosphere.
In addition, attempts at corroboration might reveal that the model is actually incorrect. Careful measurements might expose the fact that the gravitational force increases as the body falls closer to earth. Very careful measurements might reveal relativistic effects. Technically, the familiar Falling Body Model is just wrong, even under excessive restrictions such as ``in a perfect vacuum'' and ``over small distances.'' But it is an incredibly useful model nonetheless.
There are several morals here.
Models need not be complete to be useful.
Models need not be perfectly accurate to be useful.
The user of a model must understand its limitations.