


Next: Superposition Assumption
Up: General Assumptions
Previous: Retinocortical Transformation
For fixed  , the kernel gives
the RF profile
, the kernel gives
the RF profile  of a cell
located at position
of a cell
located at position 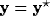 , i.e., how the input stimulus
is weighted in determining the output excitation of the cell at position
, i.e., how the input stimulus
is weighted in determining the output excitation of the cell at position
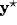 .
The RF profiles
.
The RF profiles  are characterized on the basis of various aspects (position, orientation,
size, sign, etc.) that determine to which type of stimuli they are
sensitive. Quantitatively, the various aspects can be related to the
values of a set of parameters
are characterized on the basis of various aspects (position, orientation,
size, sign, etc.) that determine to which type of stimuli they are
sensitive. Quantitatively, the various aspects can be related to the
values of a set of parameters  characterizing the RF.
In general, their space-variant distribution over the cortical surface can be
expressed through parametric mappings
[76] and the kernel can be rewritten in a more
[98] explicit form:
characterizing the RF.
In general, their space-variant distribution over the cortical surface can be
expressed through parametric mappings
[76] and the kernel can be rewritten in a more
[98] explicit form:
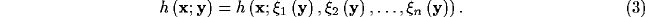
The dependencies of the kernel  on the cortical coordinates
on the cortical coordinates
 , described by the parametric maps
, described by the parametric maps  , shows how,
changing position on cortical plane, RFs vary in orientation specificity, position in the visual field,
overlapping, field size, contrast sensitivity, etc
[2,13,59,60,95,107,127]. In the following, we shall focus on variations of position and orientation.
, shows how,
changing position on cortical plane, RFs vary in orientation specificity, position in the visual field,
overlapping, field size, contrast sensitivity, etc
[2,13,59,60,95,107,127]. In the following, we shall focus on variations of position and orientation.
Exploiting the concept of topographic mapping
[76,115],
[75,114] each point in the visual
field can be assigned to a point in the cortical plane by
means of a transformation
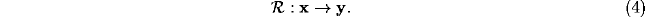
 is assumed to be bijective, hence, to find the position
is assumed to be bijective, hence, to find the position  in the visual
field in which the RF of a certain neuron in
in the visual
field in which the RF of a certain neuron in  is
centered, it is sufficient to follow backwards the transformation
is
centered, it is sufficient to follow backwards the transformation  .
.
Orientation varies jointly with the cell's position on the cortical plane
according to the orientation map

so that every point of cortical surface has associated with it a preferred
orientation  ranging from 0 to
ranging from 0 to  [6,8,12,127].
In this case, given
[6,8,12,127].
In this case, given  and
and
 , the properties of the kernel
, the properties of the kernel  are summarized, through the rototranslation transformation, by
the function
are summarized, through the rototranslation transformation, by
the function 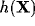 :
:
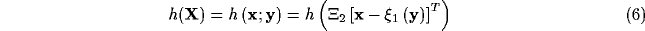
where

is the rotation matrix for the angle  .
.
Under these assumptions, the distribution of excitation

provides a mixed spatial representation of both stimulus
position and orientation.



Next: Superposition Assumption
Up: General Assumptions
Previous: Retinocortical Transformation
 , the kernel gives
the RF profile
, the kernel gives
the RF profile  of a cell
located at position
of a cell
located at position  , i.e., how the input stimulus
is weighted in determining the output excitation of the cell at position
, i.e., how the input stimulus
is weighted in determining the output excitation of the cell at position
 .
The RF profiles
.
The RF profiles  are characterized on the basis of various aspects (position, orientation,
size, sign, etc.) that determine to which type of stimuli they are
sensitive. Quantitatively, the various aspects can be related to the
values of a set of parameters
are characterized on the basis of various aspects (position, orientation,
size, sign, etc.) that determine to which type of stimuli they are
sensitive. Quantitatively, the various aspects can be related to the
values of a set of parameters  characterizing the RF.
In general, their space-variant distribution over the cortical surface can be
expressed through parametric mappings
[76] and the kernel can be rewritten in a more
[98] explicit form:
characterizing the RF.
In general, their space-variant distribution over the cortical surface can be
expressed through parametric mappings
[76] and the kernel can be rewritten in a more
[98] explicit form:



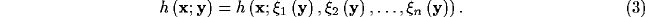
 on the cortical coordinates
on the cortical coordinates
 , described by the parametric maps
, described by the parametric maps  , shows how,
changing position on cortical plane, RFs vary in orientation specificity, position in the visual field,
overlapping, field size, contrast sensitivity, etc
[
, shows how,
changing position on cortical plane, RFs vary in orientation specificity, position in the visual field,
overlapping, field size, contrast sensitivity, etc
[
 is assumed to be bijective, hence, to find the position
is assumed to be bijective, hence, to find the position  in the visual
field in which the RF of a certain neuron in
in the visual
field in which the RF of a certain neuron in  is
centered, it is sufficient to follow backwards the transformation
is
centered, it is sufficient to follow backwards the transformation  .
.

 ranging from 0 to
ranging from 0 to  [
[ and
and
 , the properties of the kernel
, the properties of the kernel  are summarized, through the rototranslation transformation, by
the function
are summarized, through the rototranslation transformation, by
the function 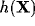 :
:
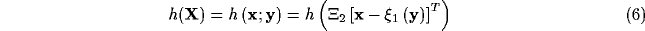

 .
.
