The computational characteristics of each neuron are not independent of the ones of other neurons laying in the same layer, rather, they are often the consequence of a collective behavior of neighboring cells. More specifically, one can assume the superposition of feed-forward and feedback contributions to investigate how information is processed through the various stages of the visual pathway. At each stage, we can identify components or computational primitives due only to feed-forward connections (e.g., afferent projections) and the properties not found in the components of a given stage can emerge from their organization and their interactions with components of the subsequent one. According to such principle, we assume that, at cortical level, simple cell RF profiles are the consequence of two main factors: (1) functional projections of LGN afferent neurons and (2) intracortical recurrent inhibition. Specifically, mechanisms similar to that proposed by Hubel and Wiesel [59] or the reported orientation bias of single geniculate neurons [100,105,117,118] provide to simple cells a weak bias in orientation, but the final profiles of the RFs are molded by inhibitory processes inside the cortex.
From the point of view of linear operator theory, this means decomposing
the operator 
into a cascade of a feed-forward operator 
and a
feed-back loop through the operator 
, as schematically depicted in
figure 1.
Figure 1: Schematic diagrams for feed-forward (left) and feed-back (right) operators
Therefore, if
is the initial excitation, the final distribution of excitation will be
where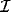 
is the identity operator, a is the excitatory gain (a>0),
that quantifies the impact of feed-forward projections, and b is a parameter that
specifies the strength and the sign of the intracortical influence (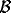
operator). Since
we'll focus our attention on the net inhibitory effects, b will be
always supposed positive.
The feed-forward operator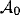 
is defined as
Recent experimental investigations
[18,109,110] have shown that simple cell RFs arise from the convergence of ON-center and OFF-center geniculate cells.
For the sake of simplicity, in the present study we
supposed a direct synaptic excitation from one type of cells only.
Functionally, the convergence of feed-forward projections of either ON- or
OFF-center cells, can be described through elliptic kernels.
Specifically,
we shall refer to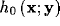 
as a
family of positive elongated Gaussians with equal size and with orientations
that vary with cortical coordinates, according to a specific orientation map.
The ``initial'' RF profile of these cells is thus
where p refers to the aspect ratio of the field, and 
specifies
the RF size.
Also the feed-back operator 
can be defined in integral term
where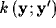 
is the kernel of intracortical
interaction.
The two-dimensional profile of the kernel 
represents the normalized distribution of intracortical spatial
coupling, referred to a fixed location on the cortical plane.
Its shape models the structural organization of inhibitory
circuits and it is thus related to the spread and morphology of dendritic
and axon arborizations of inhibitory interneurons.
