In the same way as the running blob is repelled by its self-inhibitory tail, it can also be attracted by excitatory input from another layer, as conveyed by a connection matrix. Imagine two layers of the same size mutually connected by the identity matrix, i.e., each neuron in one layer is connected only with the one corresponding neuron in the other layer having the same index value. The input then is a copy of the blob of the other layer. This favors alignment between the blobs, because then they can cooperate and stabilize each other. This synchronization principle holds also in the presence of the noisy connection matrices generated by real image data (see Figure 4). The corresponding equation is (cf. Equation 1):
The two layers are indicated by the indices 
and
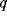. The synaptic weights of the connections are 
, and the
strength of mutual interaction is controlled by the parameter
. (The reason why we use the maximum function
instead of the usual sum will be discussed in
the Maximum versus... section.)
Figure 4: (click on the image to view a larger version) Synchronization between two
running blobs as simulated with
Equations 13 and
14. Layer input as well as the
internal layer state 
is shown at an early stage, in which the
blobs of two layers are not yet aligned, left, and at a later state,
right, when they are aligned. The two layers are of different size,
and the region in layer 1 that correctly maps to layer 2 is indicated
by a square defined by the dashed line. In the early non-aligned
case one can see that the blobs are smaller and not at the location
of maximal input. The locations of maximal input indicate where the
actual corresponding neurons of the blob of the other layer are. In
the aligned case the blobs are larger and at the locations of high
layer input.
