For performance reasons, it is often important to partition the linear algebra object on a template block boundary (e.g. when it is necessary to guarantee that a specific sub-matrix or sub-vector exists entirely on one node). To determine the size that can be split on a given side of an object, we provide the call place HR here
![]()
![]()
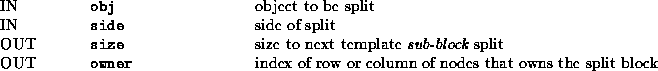
place HR here This call returns the size to the nearest block boundary on the specified side. The sides that can be specified are
![]()
Depending on which side is indicated and the object type of obj, the index returned in owner has the meaning given Table 3.1.
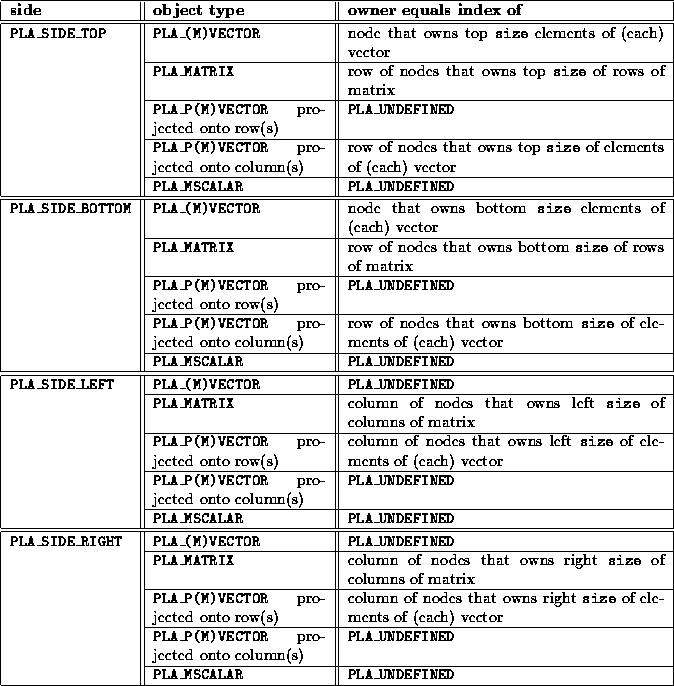
Table 3.1: Value of owner returned by the call
PLA_Obj_split_size( obj, side, &size, &owner );.
Note: It is important to realize that the size returned in size is to the next boundary, which doesn't necessarily imply that the blocks to the left and right of this boundary exist on different nodes. Indeed, a boundary of between nodes will always occur on a block boundary, but not necessarily vice versa. This allows us to generalize the creation of templates in the future, without requiring a change in codes written using the PLAPACK infrastructure. The assumption is that template blocks always exist entirely in one node, a column of template blocks always exists within one column of nodes, and a row of template blocks always exists within one row of nodes.