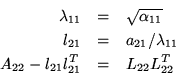 An algorithm for computing the Cholesky factorization is
now given by
An algorithm for computing the Cholesky factorization is
now given by
The right-looking algorithm for implementing this operation can be described
by partitioning the matrices
![]() where
where ![]() and
and ![]() are scalars.
As a result,
are scalars.
As a result, ![]() and
and ![]() are vectors of length n-1 , and
are vectors of length n-1 , and
![]() and
and ![]() are matrices of size
are matrices of size ![]() .The
.The ![]() indicates the symmetric part of A , which will not
be updated.
Now,
indicates the symmetric part of A , which will not
be updated.
Now,
![]() From this we derive the equations
From this we derive the equations
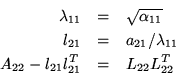 An algorithm for computing the Cholesky factorization is
now given by
An algorithm for computing the Cholesky factorization is
now given by
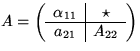
One question that may be asked about the above algorithm is
what is stored in the matrix after k
steps.
We answer this by partitioning
![]() where
where ![]() and
and ![]() are
are ![]() .Here ``TL '' , ``BL '', and ``BR '' stand for
``Top-Left'', ``Bottom-Left'', and ``Bottom-Right'', respectively.
As seen before
.Here ``TL '' , ``BL '', and ``BR '' stand for
``Top-Left'', ``Bottom-Left'', and ``Bottom-Right'', respectively.
As seen before
![]() so that
so that
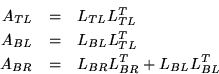 It can be easily verified that
the above algorithm has the effect that after k
steps
It can be easily verified that
the above algorithm has the effect that after k
steps
The bulk of the computation in the above algorithm
is in the symmetric rank-1 update, which performs
![]() operations on
operations on ![]() data.
It is this ratio of computation to data volume (requiring
memory accesses) that stands in the way of high
performance. To overcome this, we now show how
to reformulate the algorithm in terms of
matrix-matrix multiplication (or rank-k updates)
which have a more favorable computation to
data volume ratio, allowing for more effective use
of a microprocessor's cache memory.
data.
It is this ratio of computation to data volume (requiring
memory accesses) that stands in the way of high
performance. To overcome this, we now show how
to reformulate the algorithm in terms of
matrix-matrix multiplication (or rank-k updates)
which have a more favorable computation to
data volume ratio, allowing for more effective use
of a microprocessor's cache memory.
Given the derivation of the basic algorithm given above, it is not difficult to derive a blocked (matrix-matrix operation based) algorithm, as is shown in Fig. 1.
Figure 1:
Similarity in the derivation
of a Level-2 (left) and Level-3 (right) BLAS based right-looking Cholesky factorization.
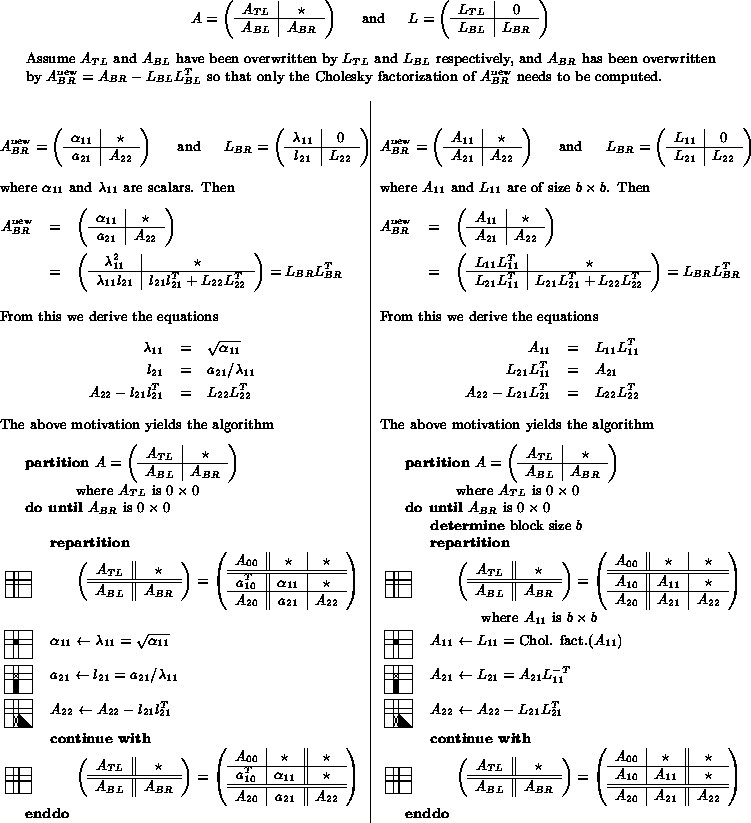
![]()
![]() (solved as triangular solve with multiple-right-hand-sides
(solved as triangular solve with multiple-right-hand-sides
![]() )
)
![]()
Fig. 2 (a)-(b) illustrate how the developed
algorithm is translated into a PLAPACK code.
It suffices to know that object A references the original
matrix to be factored. Object ABR is a view into the current
part of the matrix that still needs to be factored (![]() in
previous discussion). The remainder of the code is self
explanatory when compared to the algorithm in (a) of that figure.
Note that the call to Chol_level2 is a
call to a basic (nonblocked) implementation of the Cholesky
factorization. That routine itself resembles the presented
code in (b) closely.
in
previous discussion). The remainder of the code is self
explanatory when compared to the algorithm in (a) of that figure.
Note that the call to Chol_level2 is a
call to a basic (nonblocked) implementation of the Cholesky
factorization. That routine itself resembles the presented
code in (b) closely.
Figure 2:
Various versions of level-3 BLAS based Cholesky factorization using
PLAPACK.

While
the code presented in Fig. 2 (b) is a straight
forward translation of the developed algorithm, it does not provide
high performance. The primary reason for this is that the
factorization of ![]() is being performed as a call to
a parallel matrix-vector based routine, which requires an extremely
large number of communications. These communications can be
avoided by choosing the size of
is being performed as a call to
a parallel matrix-vector based routine, which requires an extremely
large number of communications. These communications can be
avoided by choosing the size of ![]() so that it exists
entirely on one node.
so that it exists
entirely on one node.
In Fig. 2 (c) we show how minor modifications
to the PLAPACK implementation in (b) allows us to force ![]() to exist on one node. To understand the optimizations,
one must have a rudimentary understanding of how matrices are
distributed by PLAPACK.
A given matrix A is partitioned like
to exist on one node. To understand the optimizations,
one must have a rudimentary understanding of how matrices are
distributed by PLAPACK.
A given matrix A is partitioned like
 For understanding the code, the sizes of the blocks are not important.
What is important is that these blocks are assigned
to an
For understanding the code, the sizes of the blocks are not important.
What is important is that these blocks are assigned
to an ![]() logical mesh of nodes using
a two-dimensional cartesian distribution:
logical mesh of nodes using
a two-dimensional cartesian distribution:
Given that the currently active submatrix ![]() is distributed to
a given logical mesh of nodes, determining a block size so
that
is distributed to
a given logical mesh of nodes, determining a block size so
that ![]() resides on one node requires us to
take the minimum of
resides on one node requires us to
take the minimum of
Notice that if ![]() exists within one node, then
exists within one node, then
![]() exists within one column of nodes.
Recognizing that
exists within one column of nodes.
Recognizing that ![]() is a row-wise operation and thus parallelizes trivially
if
is a row-wise operation and thus parallelizes trivially
if ![]() is duplicated within the column that owns
is duplicated within the column that owns
![]() (and thus
(and thus ![]() ),
a further optimization is attained by duplicating
),
a further optimization is attained by duplicating ![]() within
the appropriate column of nodes, and performing the update of
within
the appropriate column of nodes, and performing the update of ![]() locally on those nodes.
The resulting PLAPACK code is given in Fig. 2 (c).
locally on those nodes.
The resulting PLAPACK code is given in Fig. 2 (c).
To understand further optimizations, one once again needs to know more about some of the principles underlying PLAPACK. Unlike ScaLAPACK, PLAPACK has a distinct approach to distributing vectors. For scalability reasons, parallel dense linear algebra algorithms must be implemented using a logical two-dimensional mesh of nodes [5,11,13,15]. However, for the distribution of vectors, that two-dimensional mesh is linearized by ordering the nodes in column-major order. Assignment of a vector to the nodes is then accomplished by partitioning the vector in blocks and wrapping these blocks onto the linear array of nodes in round-robin fashion. Assignment of matrices is then dictated by the following principle:
Note that as a consequence of the last optimization,
all computation required to factor ![]() and update
and update ![]() is performed within one column
of nodes. This is an operation that is very much
in the critical path, and thus contributes considerably
to the overall time required for the Cholesky factorization.
If one views the panel of the matrix
is performed within one column
of nodes. This is an operation that is very much
in the critical path, and thus contributes considerably
to the overall time required for the Cholesky factorization.
If one views the panel of the matrix
![]() as a collection (panel) of columns, then
by simultaneously scattering the elements of these columns
of matrices
within rows of nodes one can redistribute the panel as a collection
of vectors (multivector).
Subsequently,
as a collection (panel) of columns, then
by simultaneously scattering the elements of these columns
of matrices
within rows of nodes one can redistribute the panel as a collection
of vectors (multivector).
Subsequently, ![]() can be factored as
a multivector and, more importantly, considerably
more parallelism can be attained during the update of
can be factored as
a multivector and, more importantly, considerably
more parallelism can be attained during the update of
![]() , since the multivector is distributed to nodes
using a one-dimensional data distribution.
, since the multivector is distributed to nodes
using a one-dimensional data distribution.
It should be noted that the volume of data communicated
when redistributing (scattering or
gathering) a panel of length n
and width b
is ![]() , where r equals the
number of rows in the mesh of nodes.
The cost of (parallel) computation subsequently performed
on the panel is
, where r equals the
number of rows in the mesh of nodes.
The cost of (parallel) computation subsequently performed
on the panel is ![]() .Thus, if the block size b is relatively large,
there is an advantage to redistributing the panel.
Furthermore, the multivector distribution is a
natural intermediate distribution for the data
movement that subsequently must be performed to
duplicate the data as part of the parallel
symmetric rank-k update [16].
A further optimization of the parallel Cholesky
factorization, for which we do not present code
in Fig. 2,
takes advantage of this fact.
.Thus, if the block size b is relatively large,
there is an advantage to redistributing the panel.
Furthermore, the multivector distribution is a
natural intermediate distribution for the data
movement that subsequently must be performed to
duplicate the data as part of the parallel
symmetric rank-k update [16].
A further optimization of the parallel Cholesky
factorization, for which we do not present code
in Fig. 2,
takes advantage of this fact.
Naturally, one may get the impression that we have merely hidden all complexity and ugliness in routines like PLA_Chol_mv. Actually, each of those routines themselves are coded at the same high level, and are not substantially more complex than the examples presented.