


Next: 4 Householder QR Factorization
Up: PLAPACK: High Performance through
Previous: 2 Cholesky Factorization
Subsections
Next, we discuss the computation of
the LU factorization
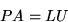 where A is an
where A is an 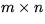 matrix, L is an
matrix, L is an 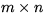 lower trapezoidal matrix with
unit diagonal, and
U is an
lower trapezoidal matrix with
unit diagonal, and
U is an 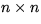 uppertriangular matrix.
P is an
uppertriangular matrix.
P is an 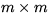 permutation matrix
which has the property that
permutation matrix
which has the property that
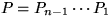 where
where 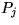 is the permutation matrix that
swaps the j th row with the pivot row during
the j th iteration of the outerloop of the algorithm.
is the permutation matrix that
swaps the j th row with the pivot row during
the j th iteration of the outerloop of the algorithm.
Let us assume that we have already computed
permutations 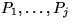 such that
such that
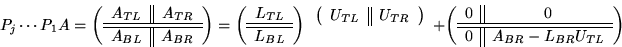 where
where 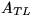 ,
, 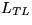 , and
, and 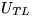 are
are 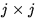 ,and the matrix has been overwritten by
,and the matrix has been overwritten by
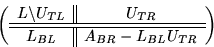
The outer-product
based variant,
implemented for example in LAPACK, for computing
the LU factorization with partial pivoting proceeds
as follows:
-
Partition
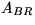 (which has been overwritten as described above)
like
(which has been overwritten as described above)
like
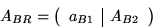 where
where 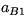 equals the first column of
equals the first column of 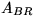 .
. -
Compute permutation
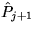 which swaps the
first and (j+1) st rows of
which swaps the
first and (j+1) st rows of 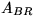 , where
the (j+1) st element in
, where
the (j+1) st element in 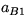 equals the element with
maximal absolute value in that vector.
equals the element with
maximal absolute value in that vector.
-
Permute
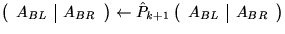 and repartition updated
and repartition updated 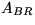 like
like
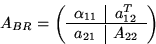
-
Update
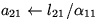 .
. -
Update
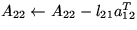 .
. -
Repartition
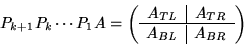 where
where 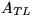 is now
is now 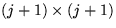 ,and
,and
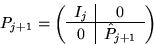
-
Continue with this new partitioning.
It can be easily shown that after the above
described steps
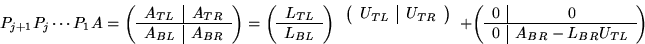 where
where 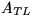 ,
, 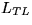 , and
, and 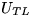 are now
are now 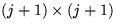 ,and the matrix has been overwritten by
,and the matrix has been overwritten by
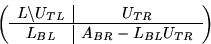 Notice that when j = 0 , the matrix contains the
original matrix, while when j = n , it has been
overwritten with the L and U factors.
Notice that when j = 0 , the matrix contains the
original matrix, while when j = n , it has been
overwritten with the L and U factors.
Given the basic algorithm described above,
it is not difficult to derive a blocked algorithm
as we show next. The result is given in
Fig. 3.
The implementation of the LU factorization in parallel using PLAPACK
closely follows the blocked algorithm discussed in the last section.
There are, however, two important differences.
First, pivoting is more complex in parallel. The pivot is determined
by a straightforward call to PLA_Iamax(). However, the
permutation of rows may require communication.
Second, on a parallel machine with cartesian deistribution, the
matrix-vector-based factoring of the left panel of columns of the
matrix may incur load imbalance (because the panel only exists within
a single column of processors.) We circumvent this load imbalance by
redistributing the panel as a PLAPACK multivector during the panel
factorization, as discussed in the section on Cholesky factorization.
With these points in mind, we present the algorithm for the parallel LU
factorization side by side with the PLAPACK code
implementation. The code for the column-by-column factorization of
the panel as multivector is not presented. It is a straightforward
translation of the algorithm presented in Section 3.3.
Figure 3:
The blocked LU factorization algorithm in PLAPACK.




Next: 4 Householder QR Factorization
Up: PLAPACK: High Performance through
Previous: 2 Cholesky Factorization
plapack@cs.utexas.edu
![]() such that
such that
![]() where
where ![]() ,
, ![]() , and
, and ![]() are
are ![]() ,and the matrix has been overwritten by
,and the matrix has been overwritten by
![]()
