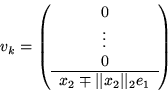 has this property. Notice that k here is used to
indicate that the first k-1 elements of x are
to be left alone, which results in
has this property. Notice that k here is used to
indicate that the first k-1 elements of x are
to be left alone, which results in To present a basic algorithm for the QR factorization, we must start by introducing Householder transforms (reflections).
Householder transforms are orthonormal transformations
that can be written as
![]() where
where ![]() . These
transformations, sometimes called reflectors,
have a number
of interesting properties:
. These
transformations, sometimes called reflectors,
have a number
of interesting properties:
![]() ,
,![]() , and
, and
![]() .Of most interest to us is the fact that given a
vector
.Of most interest to us is the fact that given a
vector ![]() , where
, where
![]() is of length k-1 , one can find
a vector
is of length k-1 , one can find
a vector ![]() such that
such that
![]() where
where
![]() .Indeed, it can be easily verified that
.Indeed, it can be easily verified that
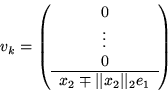 has this property. Notice that k here is used to
indicate that the first k-1 elements of x are
to be left alone, which results in
has this property. Notice that k here is used to
indicate that the first k-1 elements of x are
to be left alone, which results in ![]() having
k-1 zero valued leading elements.
The sign that is chosen corresponds to the sign of the
first entry of
having
k-1 zero valued leading elements.
The sign that is chosen corresponds to the sign of the
first entry of ![]() to avoid catastrophic cancellation.
Vector
to avoid catastrophic cancellation.
Vector ![]() can be scaled arbitrarily
by adjusting
can be scaled arbitrarily
by adjusting ![]() correspondingly. In the subsequent section,
we will scale it so that the first nonzero ( k th) entry of
correspondingly. In the subsequent section,
we will scale it so that the first nonzero ( k th) entry of ![]() is
1 .
is
1 .
To compute the QR factorization of given ![]() matrix A ,
we wish to compute Householder transformations
matrix A ,
we wish to compute Householder transformations
![]() such that
such that
![]() where R is uppertriangular.
where R is uppertriangular.
An algorithm for computing the QR factorization is given by
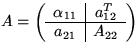
In [3,9], it is shown how
a blocked (matrix-matrix multiply)
based algorithm can be derived ,
by creating a WY transform,
which, when applied, yield the same result as a number
of successive applications of Householder transforms:
![]() where W and Y are both
where W and Y are both ![]() .Given the k vectors that define the k
Householder transforms, these
matrices can be computed one column at a time
in a relatively straight forward manner.
.Given the k vectors that define the k
Householder transforms, these
matrices can be computed one column at a time
in a relatively straight forward manner.
Given the WY transform discussion above, the blocked version of the algorithm is given in Fig. 4.
The expert optimization of the QR factorization lies in the ability of PLAPACK of viewing parts of the matrix as a panel that can be redistributed as a multivector on the nodes. A PLAPACK implementation that explores this is given in Fig. 4.
Figure 4:
Optimized implementation of QR factorization using PLAPACK
