
Table 3: OPR and OPL behavior specification.
In this section we present the results of empirically testing how the complete behavior performs when using the different RCF options. Since the behaviors differ only in their RCFs, we refer below to, for example, ``the complete behavior with the DT RCF'' simply as ``the DT RCF.'' Also presented are empirical results verifying the advantage of reasoning about action-execution time.
In order to test the different RCFs, we created a team formation that emphasizes the advantage of passing to some teammates over others. When both teams use the standard formation (that of the black team in Figure 2), every player is covered by one opponent. However, this situation is an artificial artifact of having the same person program both teams. Ideally, the players would have the ability to move to open positions on the field. However at this point, such functionality represents future work (see Section 5). Instead, in order to reflect the fact that some players are typically more open than others, we tested the RCFs against the OPR--Only Play Right--formation which is illustrated by the white team in Figure 2. We also used the symmetrical OPL-Only Play Left--formation for testing. These behaviors are specified in Table 3.

Table 3: OPR and OPL behavior specification.
During testing, each run consists of 34 five-minute games between a pair of teams. We tabulate the cumulative score both in total goals and in games won (ties are not broken) as in Table 4. Graphs record the difference in cumulative goals scored (Figure 3) and games won (Figure 4) as the run progresses.
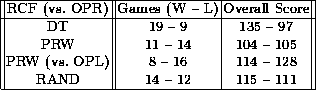
Table 4: Results are cumulative over 34 five-minute games: ties are
not broken. Unless otherwise indicated, the opponent--whose score
always appears second--uses the OPR formation.
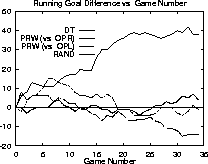
Figure 3: The differences in cumulative goals as the runs progress.
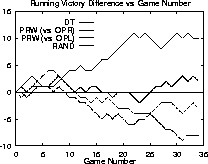
Figure 4: The differences in cumulative games won as the runs progress.
In order to test the effectiveness of the DT RCF, we compared its performance against the performance of the PRW and RAND RCFs when facing the same opponent: OPR. While the DT and RAND RCFs are symmetrical in their decision making, the PRW RCF gives preference to one side of the field and therefore has an advantage against the OPR strategy. Thus we also include the results of the PRW RCF when it faces the symmetrical opponent: OPL. From the table and the graphs, it is apparent that the DT RCF is an effective method of decision making in this domain.
In order to test the effectiveness of the reasoning about action-execution time, we compared the performance of the standard DT RCF against that of the same RCF with the assumption that there is never an opponent nearby: even if there is, the RCF ignores it. This assumption affects Steps 4 and 6 of the RCF specification in Table 1. Both RCFs are played against the OPR behavior. As apparent from Table 5, the reasoning about action-execution time makes a significant difference.

Table 5: No-rush DT is the same RCF as the standard DT except
that there is no reasoning about action-execution time. The Standard
DT RCF performs significantly better.
We expect that the DT RCF, including the reasoning about
action-execution time, will perform favorably against teams that cover
our players unevenly so that the DT can find an open player to whom to
pass. Indeed, it was used successfully as part of the CMUnited
simulator team at RoboCup-97 [5] which was held at
IJCAI-97. In a field of 29 teams, CMUnited made it to the semi-finals,
before losing to the eventual champions![]() .
.