Skip to main content

Subsection 2.2.6 Change of orthonormal basis

Homework 2.2.6.1.

Consider the vector \(x = \left( \begin{array}{r} -2 \\ 1 \end{array} \right)\) and the following picture that depicts a rotated basis with basis vectors \(u_0 \) and \(u_1 \text{.}\)

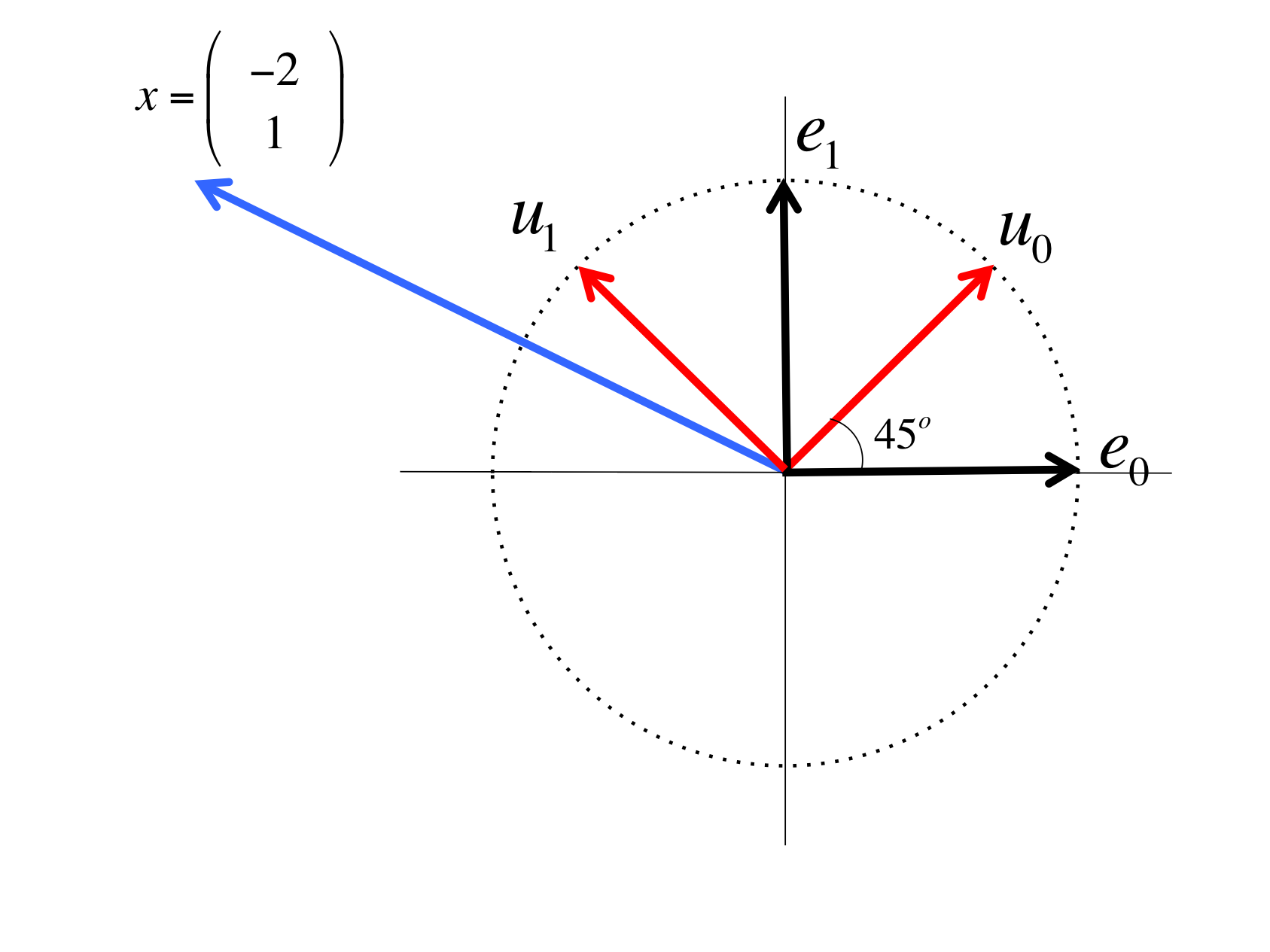
What are the coordinates of the vector \(x \) in this rotated system? In other words, find \(\widehat x = \left( \begin{array}{c} \widehat \chi_0 \\ \widehat \chi_1 \end{array} \right) \) such that \(\widehat \chi_0 u_0 + \widehat \chi_1 u_1 = x \text{.}\)

Solution

There are a number of approaches to this. One way is to try to remember the formula you may have learned in a pre-calculus course about change of coordinates. Let's instead start by recognizing (from geometry or by applying the Pythagorean Theorem) that

\begin{equation*} u_0 = \left( \begin{array}{c} \sqrt{2}/2 \\ \sqrt{2}/2 \end{array} \right) = \frac{\sqrt{2}}{2} \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \quad \mbox{and} \quad u_1 = \left( \begin{array}{c} -\sqrt{2}/2 \\ \sqrt{2}/2 \end{array} \right) = \frac{\sqrt{2}}{2} \left( \begin{array}{c} -1 \\ 1 \end{array} \right) . \end{equation*}

Here are two ways in which you can employ what you have discovered in this course:

  • Since \(u_0 \) and \(u_1 \) are orthonormal vectors, you know that

    \begin{equation*} \begin{array}{l} x \\ ~~~=~~~~ \lt u_0 \mbox{ and } u_1 \mbox{ are orthonormal } \gt \\ \begin{array}[t]{c} \underbrace{ ( u_0^T x ) u_0 }\\ \mbox{ component in the } \\ \mbox{ direction of } u_0 \end{array} + \begin{array}[t]{c} \underbrace{ ( u_1^T x ) u_1 }\\ \mbox{ component in the } \\ \mbox{ direction of } u_1 \end{array} \\ ~~~=~~~~ \lt \mbox{ instantiate } u_0 \mbox{ and } u_1 \gt \\ \left( \frac{\sqrt{2}}{2} \left( \begin{array}{c} 1 \\ 1 \end{array} \right)^T \left( \begin{array}{c} -2 \\ 1 \end{array} \right) \right) u_0 + \left( \frac{\sqrt{2}}{2} \left( \begin{array}{c} -1 \\ 1 \end{array} \right)^T \left( \begin{array}{c} -2 \\ 1 \end{array} \right) \right) u_1\\ ~~~ = ~~~~ \lt \mbox{ evaluate } \gt \\ - \frac{\sqrt{2}}{2} u_0 + \frac{3\sqrt{2}}{2} u_1. \end{array} \end{equation*}

  • An alternative way to arrive at the same answer that provides more insight. Let \(U = \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \text{.}\) Then

    \begin{equation*} \begin{array}{l} x \\ ~~~ = ~~~~ \lt U \mbox{ is unitary (or orthogonal since it is real valued)} \gt \\ U U^T x \\ ~~~ = ~~~~ \lt \mbox{ instantiate } U \gt \\ \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \left( \begin{array}{c} u_0^T \\ \hline u_1^T \end{array} \right) x \\ ~~~ = ~~~~ \lt \mbox{ matrix-vector multiplication } \gt \\ \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \left( \begin{array}{c} u_0^T x \\ \hline u_1^T x \end{array} \right) \\ ~~~ = ~~~~ \lt \mbox{ instantiate } \gt \\ \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \left( \begin{array}{c} \frac{\sqrt{2}}{2} \left( \begin{array}{c}1 \\ 1 \end{array} \right)^T \left( \begin{array}{c} -2 \\ 1 \end{array} \right) \\ \frac{\sqrt{2}}{2} \left( \begin{array}{c}-1 \\ 1 \end{array} \right)^T \left( \begin{array}{c} -2 \\ 1 \end{array} \right) \end{array} \right)\\ ~~~ = ~~~~ \lt \mbox{ evaluate } \gt \\ \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \left( \begin{array}{c} -\frac{\sqrt{2}}{2} \\ \frac{3 \sqrt{2}}{2} \end{array} \right) \\ ~~~ = ~~~~ \lt \mbox{ simplify } \gt \\ \left( \begin{array}{c | c} u_0 \amp u_1 \end{array} \right) \left( \frac{\sqrt{2}}{2} \left( \begin{array}{c} -1 \\ 3 \end{array} \right) \right) \end{array} \end{equation*}

Below we compare side-by-side how to describe a vector \(x\) using the standard basis vectors \(e_0, \ldots , e_{m-1} \) (on the left) and vectors \(u_0, \ldots , u_{m-1} \) (on the right):

The vector \(x = \left( \begin{array}{c} \chi_0^{\phantom{T}} \\ \vdots \\ \chi_{m-1}^{\phantom{T}} \end{array} \right)\) describes the vector \(x \) in terms of the standard basis vectors \(e_0, \ldots , e_{m-1} \text{:}\)

\begin{equation*} \begin{array}{l} x \\ ~~~=~~~~ \lt x = I x = I I x = I I^T x \gt \\ I I^T x \\ ~~~=~~~~ \lt \mbox{ expose columns of } I \gt \\ \left( \begin{array}{c | c | c } e_0 \amp \cdots \amp e_{m-1} \end{array} \right) \left( \begin{array}{c} e_0^T \\ \hline \vdots \\ \hline e_{m-1}^T \end{array} \right) x \\ ~~~=~~~~ \lt \mbox{ evaluate } \gt \\ \left( \begin{array}{c | c | c } e_0 \amp \cdots \amp e_{m-1} \end{array} \right) \left( \begin{array}{c} e_0^T x \\ \hline \vdots \\ \hline e_{m-1}^T x \end{array} \right) \\ ~~~=~~~~ \lt e_j^T x = \chi_j \gt \\ \left( \begin{array}{c | c | c } e_0 \amp \cdots \amp e_{m-1} \end{array} \right) \left( \begin{array}{c} \chi_0 \\ \hline \vdots \\ \hline \chi_{m-1} \end{array} \right) \\ ~~~=~~~~ \lt \mbox{ evaluate } \gt \\ \chi_0 e_0 + \chi_1 e_1 + \cdots + \chi_{m-1} e_{m-1}. \end{array} \end{equation*}

Illustration:

\begin{equation*} \begin{array}{c|c} ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \\ ~\amp~ \end{array} \end{equation*}

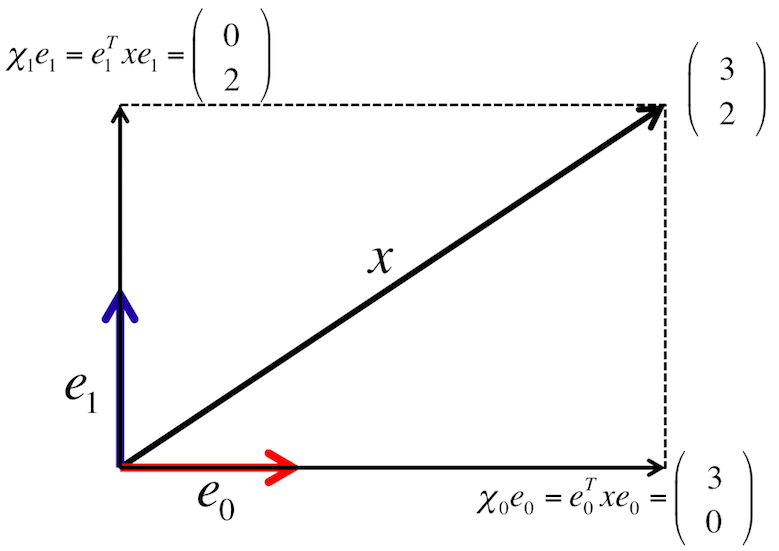
The vector \(\widehat x = \left( \begin{array}{c} u_0^T x \\ \vdots \\ u_{m-1}^T x \end{array} \right)\) describes the vector \(x \) in terms of the orthonormal basis \(u_0, \ldots , u_{m-1} \text{:}\)

\begin{equation*} \begin{array}{l} x \\ ~~~=~~~~ \lt x = I x = U U^H x \gt \\ U U^H x \\ ~~~=~~~~ \lt \mbox{ expose columns of } U \gt \\ \left( \begin{array}{c | c | c } u_0 \amp \cdots \amp u_{m-1} \end{array} \right) \left( \begin{array}{c} u_0^H \\ \hline \vdots \\ \hline u_{m-1}^H \end{array} \right) x \\ ~~~=~~~~ \lt \mbox{ evaluate } \gt \\ \left( \begin{array}{c | c | c } u_0 \amp \cdots \amp u_{m-1} \end{array} \right) \left( \begin{array}{c} u_0^H x \\ \hline \vdots \\ \hline u_{m-1}^H x \end{array} \right) \\ \phantom{ ~~~=~~~~ \lt e_j^T x = \chi_j \gt} \\ \phantom{\left( \begin{array}{c | c | c } e_0 \amp \cdots \amp e_{m-1} \end{array} \right) \left( \begin{array}{c} \chi_0 \\ \hline \vdots \\ \hline \chi_{m-1} \end{array} \right) } \\ ~~~=~~~~ \lt \mbox{ evaluate } \gt \\ u_0^H x u_0 + u_1^H x u_1 + \cdots + u_{m-1}^H x u_{m-1}. \end{array} \end{equation*}

Illustration (\(q \) should be \(u\) here):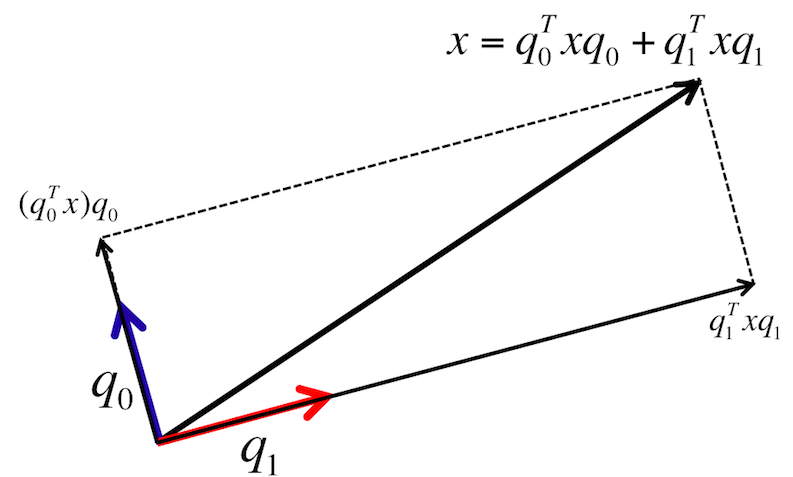

Another way of looking at this is that if \(u_0, u_1, \ldots , u_{m-1}\) is an orthonormal basis for \(\C^m \text{,}\) then any \(x\in \C^m \) can be written as a linear combination of these vectors:

\begin{equation*} x = \alpha_0 u_0 + \alpha_1 u_1 + \cdots + \alpha_{m-1} u_{m-1}. \end{equation*}

Now,

\begin{equation*} \begin{array}{rcl} u_i^H x \amp=\amp u_i^H ( \alpha_0 u_0 + \alpha_1 u_1 + \cdots + \alpha_{i-1} u_{i-1} + \alpha_i u_i + \alpha_{i+1} u_{i+1} + \cdots + \alpha_{m-1} u_{m-1} ) \\ \amp=\amp \alpha_0 \begin{array}[t]{c} \underbrace{ u_i^H u_0 } \\ 0 \end{array} + \alpha_1 \begin{array}[t]{c} \underbrace{ u_i^H u_1 } \\ 0 \end{array} + \cdots + \alpha_{i-1} \begin{array}[t]{c} \underbrace{ u_i^H u_{i-1} } \\ 0 \end{array} \\ \amp \amp ~~~~~~~~~~~~~~~~~~ + \alpha_i \begin{array}[t]{c} \underbrace{ u_i^H u_i } \\ 1 \end{array} + \alpha_{i+1} \begin{array}[t]{c} \underbrace{ u_i^H u_{i+1} } \\ 0 \end{array} + \cdots + \alpha_{m-1} \begin{array}[t]{c} \underbrace{ u_i^H u_{m-1} } \\ 0 \end{array} \\ \amp = \amp \alpha_i . \end{array} \end{equation*}

Thus \(u_i^H x = \alpha_i \text{,}\) the coefficient that multiplies \(u_i \text{.}\)

Remark 2.2.6.1.

The point is that given vector \(x \) and unitary matrix \(U \text{,}\) \(U^H x \) computes the coefficients for the orthonormal basis consisting of the columns of matrix \(U \text{.}\) Unitary matrices allow one to elegantly change between orthonormal bases.

login