Subsection 4.3.1 The SVD and the four fundamental spaces
¶Theorem 4.3.1.1.
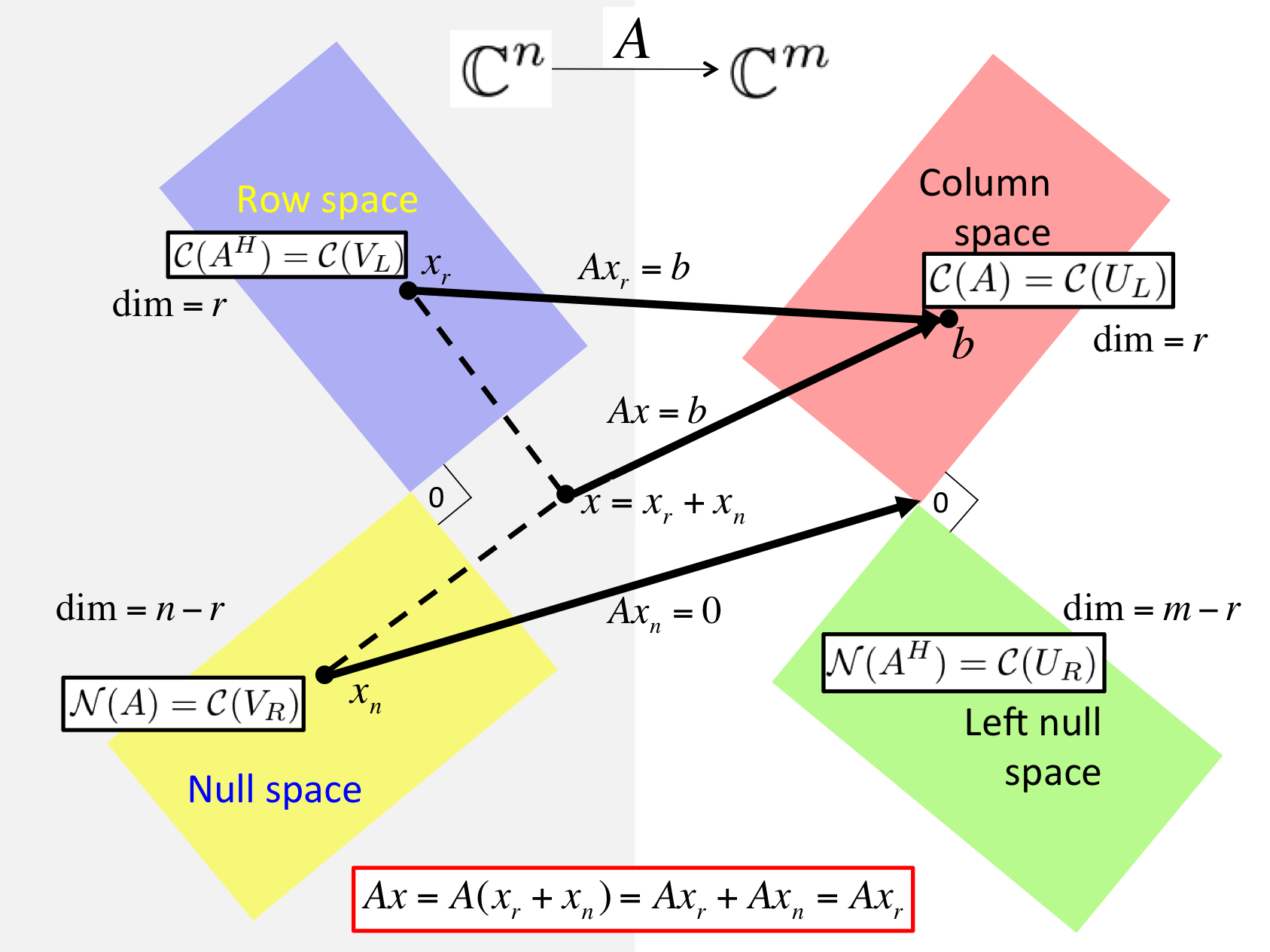
Given \(A \in \C^{m \times n}\text{,}\) let \(A = U_L \Sigma_{TL} V_L^H \) equal its Reduced SVD and \(A = \left( \begin{array}{c | c} U_L \amp U_R \end{array} \right) \left( \begin{array}{c | c} \Sigma_{TL} \amp 0 \\ \hline 0 \amp 0 \end{array} \right) \left( \begin{array}{c | c} V_L \amp V_R \end{array} \right)^H \) its SVD. Then
\(\Col( A ) = \Col( U_L ) \text{,}\)
\(\Null( A ) = \Col( V_R ) \text{,}\)
\(\Rowspace( A ) = \Col( A^H ) = \Col( V_L ) \text{,}\) and
\(\Null( A^H ) = \Col( U_R ) \text{.}\)
Proof.
We prove that \(\Col( A ) = \Col( U_L ) \text{,}\) leaving the other parts as exercises.
Let \(A = U_L \Sigma_{TL} V_L^H \) be the Reduced SVD of \(A \text{.}\) Then
\(U_L^H U_L = I \) (\(U_L \) is orthonormal),
\(V_L^H V_L = I \) (\(V_L \) is orthonormal), and
\(\Sigma_{TL} \) is nonsingular because it is diagonal and the diagonal elements are all nonzero.
We will show that \(\Col(A) = \Col( U_L ) \) by showing that \(\Col(A) \subset \Col( U_L ) \) and \(\Col(U_L) \subset \Col( A ) \)
-
\(\Col(A) \subset \Col( U_L ) \text{:}\)
Let \(z \in \Col(A) \text{.}\) Then there exists a vector \(x \in \Cn \) such that \(z = A x \text{.}\) But then \(z = A x = U_L \Sigma_{TL} V_L^H x = U_L \begin{array}[t]{c} \underbrace{\Sigma_{TL} V_L^H x}\\ \widehat x \end{array} = U_L \widehat x \text{.}\) Hence \(z \in \Col( U_L ) \text{.}\)
-
\(\Col(U_L) \subset \Col(A) \text{:}\)
Let \(z \in \Col(U_L) \text{.}\) Then there exists a vector \(x \in \C^r \) such that \(z = U_L x \text{.}\) But then \(z = U_L x = U_L \begin{array}[t]{c} \underbrace{ \Sigma_{TL} V_L^H V_L \Sigma_{TL}^{-1}}\\ I \end{array} x = A \begin{array}[t]{c} \underbrace{ V_L \Sigma_{TL}^{-1} x}\\ \widehat x \end{array} = A \widehat x \text{.}\) Hence \(z \in \Col( A ) \text{.}\)
We leave the other parts as exercises for the learner.
Homework 4.3.1.1.
For the last theorem, prove that \(\Rowspace( A ) = \Col( A^H ) = \Col( V_L ) \text{.}\)
\(\Rowspace( A ) = \Col( V_L ) \text{:}\)
The slickest way to do this is to recognize that if \(A = U_L \Sigma_{TL} V_L^H \) is the Reduced SVD of \(A \) then \(A^H = V_L \Sigma_{TL} U_L^H \) is the Reduced SVD of \(A^H \text{.}\) One can then invoke the fact that \(\Col( A ) = \Col( U_L ) \) where in this case \(A \) is replaced by \(A^H \) and \(U_L \) by \(V_L \text{.}\)
Ponder This 4.3.1.2.
For the last theorem, prove that \(\Null( A^H ) = \Col( U_R ) \text{.}\)
Homework 4.3.1.3.
Given \(A \in \C^{m \times n}\text{,}\) let \(A = U_L \Sigma_{TL} V_L^H \) equal its Reduced SVD and \(A = \left( \begin{array}{c | c} U_L \amp U_R \end{array} \right) \left( \begin{array}{c | c} \Sigma_{TL} \amp 0 \\ \hline 0 \amp 0 \end{array} \right) \left( \begin{array}{c | c} V_L \amp V_R \end{array} \right)^H \) its SVD, and \(r = \rank( A ) \text{.}\)
ALWAYS/SOMETIMES/NEVER: \(r = \rank( A ) = \dim( \Col( A ) ) = \dim( \Col( U_L ) ) \text{,}\)
ALWAYS/SOMETIMES/NEVER: \(r = \dim( \Rowspace( A ) ) = \dim( \Col( V_L ) ) \text{,}\)
ALWAYS/SOMETIMES/NEVER: \(n-r = \dim( \Null( A ) ) = \dim( \Col( V_R) ) \text{,}\) and
ALWAYS/SOMETIMES/NEVER: \(m-r = \dim( \Null( A^H ) ) = \dim( \Col( U_R ) ) \text{.}\)
ALWAYS: \(r = \rank( A ) = \dim( \Col( A ) ) = \dim( \Col( U_L ) ) \text{,}\)
ALWAYS: \(r = \dim( \Rowspace( A ) ) = \dim( \Col( V_L ) ) \text{,}\)
ALWAYS: \(n-r = \dim( \Null( A ) ) = \dim( \Col( V_R) ) \text{,}\) and
ALWAYS: \(m-r = \dim( \Null( A^H ) ) = \dim( \Col( U_R ) ) \text{.}\)
Now prove it.
-
ALWAYS: \(r = \rank( A ) = \dim( \Col( A ) ) = \dim( \Col( U_L ) ) \text{,}\)
The dimension of a space equals the number of vectors in a basis. A basis is any set of linearly independent vectors such that the entire set can be created by taking linear combinations of those vectors. The rank of a matrix is equal to the dimension of its columns space which is equal to the dimension of its row space.
Now, clearly the columns of \(U_L \) are linearly independent (since they are orthonormal) and form a basis for \(\Col( U_L ) \text{.}\) This, together with Theorem 4.3.1.1, yields the fact that \(r = \rank( A ) = \dim( \Col( A ) ) = \dim( \Col( U_L ) ) \text{.}\)
-
ALWAYS: \(r = \dim( \Rowspace( A ) ) = \dim( \Col( V_L ) ) \text{,}\)
There are a number of ways of reasoning this. One is a small modification of the proof that \(r = \rank( A ) = \dim( \Col( A ) ) = \dim( \Col( U_L ) ) \text{.}\) Another is to look at \(A^H \) and to apply the last subproblem.
-
ALWAYS: \(n-r = \dim( \Null( A ) ) = \dim( \Col( V_R) ) \text{.}\)
We know that \(\dim( \Null( A ) ) + \dim( \Rowspace( A ) ) = n \text{.}\) The answer follows directly from this and the last subproblem.
-
ALWAYS: \(m-r = \dim( \Null( A^H ) ) = \dim( \Col( U_R ) ) \text{.}\)
We know that \(\dim( \Null( A^H ) ) + \dim( \Col( A ) ) = m \text{.}\) The answer follows directly from this and the first subproblem.
Homework 4.3.1.4.
Given \(A \in \C^{m \times n}\text{,}\) let \(A = U_L \Sigma_{TL} V_L^H \) equal its Reduced SVD and \(A = \left( \begin{array}{c | c} U_L \amp U_R \end{array} \right) \left( \begin{array}{c | c} \Sigma_{TL} \amp 0 \\ \hline 0 \amp 0 \end{array} \right) \left( \begin{array}{c | c} V_L \amp V_R \end{array} \right)^H \) its SVD.
Any vector \(x \in \Cn \) can be written as \(x = x_r + x_n \) where \(x_r \in \Col( V_L ) \) and \(x_n \in \Col( V_R ) \text{.}\)
TRUE/FALSE
TRUE
Now prove it!
images/Chapter04/FundamentalSpacesSVD.pptx