Unit 2.4.3 Details
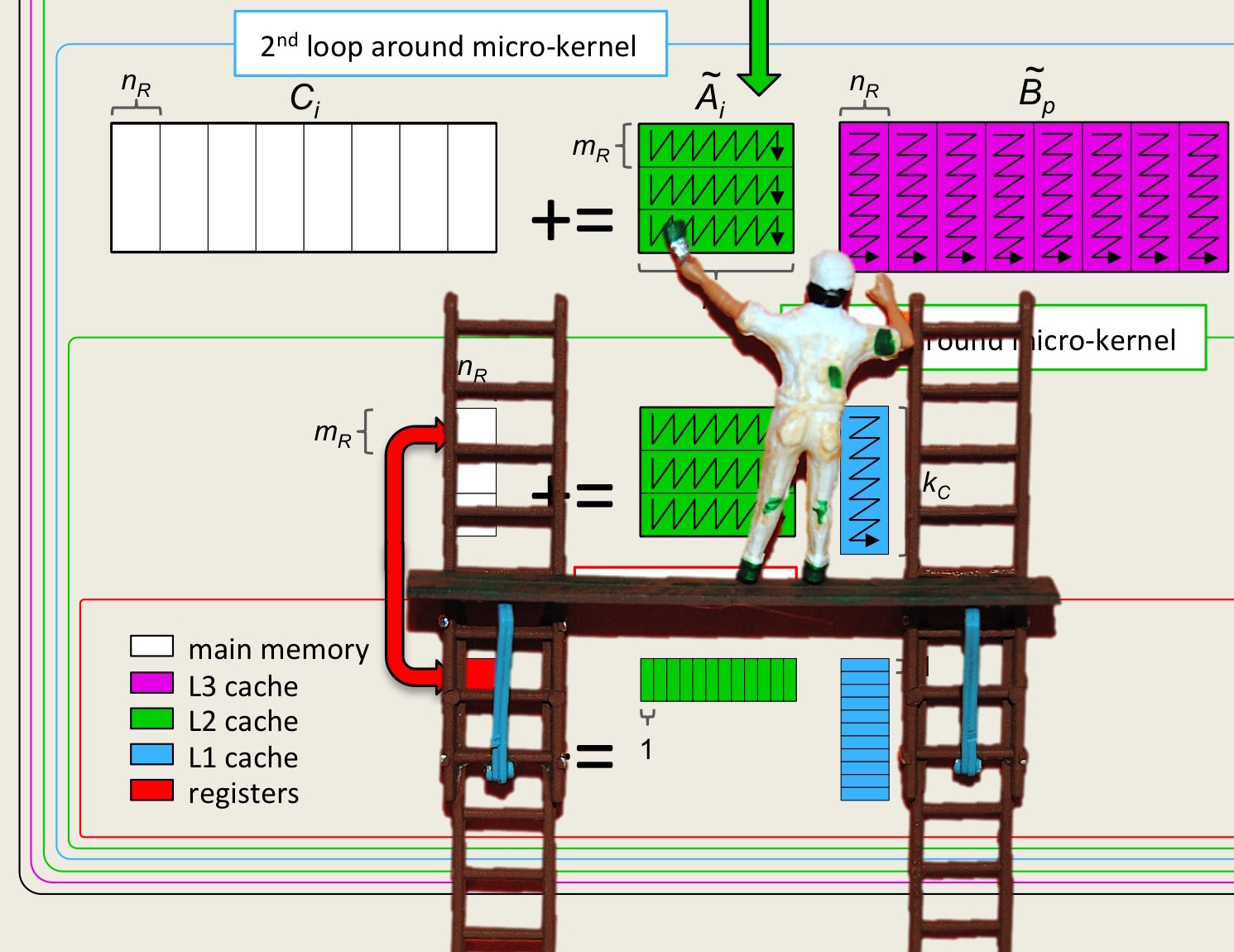
¶In this unit, we give details regarding the partial code in Figure 2.4.3 and illustrated in Figure 2.4.4.
To use the intrinsic functions, we start by including the header file immintrin.h.
#include <immintrin.h>
The declaration
__m256d gamma_0123_0 = _mm256_loadu_pd( &gamma( 0,0 ) );creates
gamma_0123_0 as a variable that references a vector register with four double precision numbers and loads it with the four numbers that are stored starting at address &gamma( 0,0 )In other words, it loads that vector register with the original values
This is repeated for the other three columns of \(C \text{:}\)
__m256d gamma_0123_1 = _mm256_loadu_pd( &gamma( 0,1 ) ); __m256d gamma_0123_2 = _mm256_loadu_pd( &gamma( 0,2 ) ); __m256d gamma_0123_3 = _mm256_loadu_pd( &gamma( 0,3 ) );
The loop in Figure 2.4.2 implements
leaving the result in the vector registers. Each iteration starts by declaring vector register variable alpha_0123_p and loading it with the contents of
__m256d alpha_0123_p = _mm256_loadu_pd( &alpha( 0,p ) );Next, \(\beta_{p,0} \) is loaded into a vector register, broadcasting (duplicating) that value to each entry in that register:
beta_p_j = _mm256_broadcast_sd( &beta( p, 0) );This variable is declared earlier in the routine as
beta_p_j because it is reused for \(j =0,1,\ldots,
\text{.}\)
The command
gamma_0123_0 = _mm256_fmadd_pd( alpha_0123_p, beta_p_j, gamma_0123_0 );then performs the computation
illustrated by
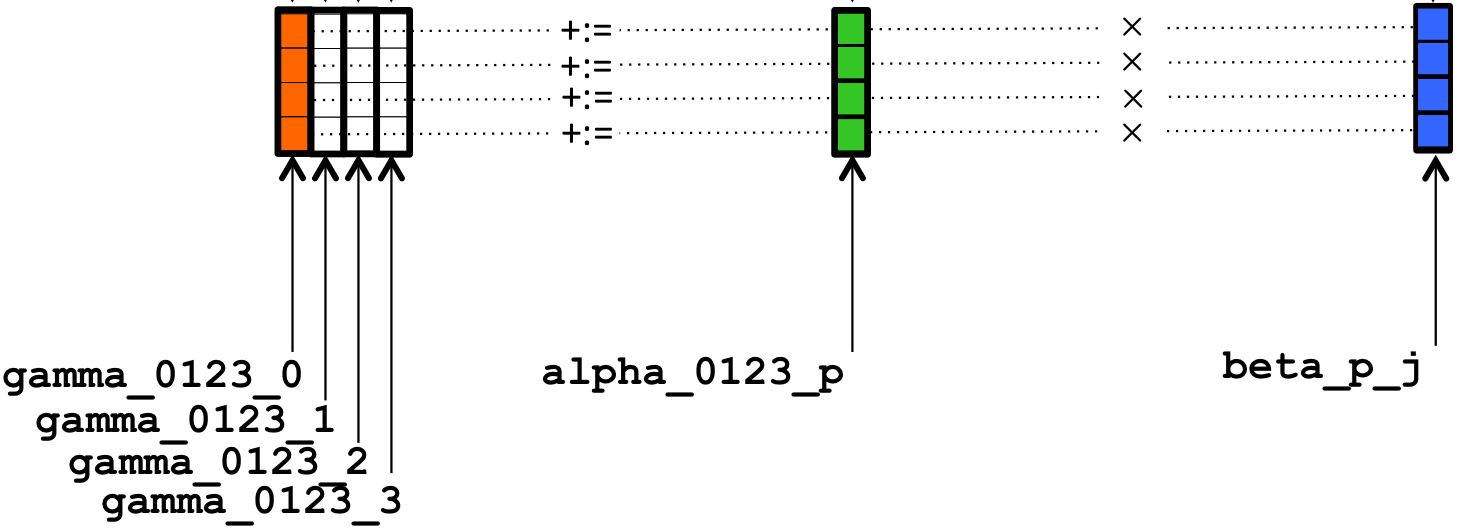
beta_p_j for \(\beta_{p,0}\) because that same vector register will be used for \(\beta_{p,j} \) with \(j = 0,1,2,3\text{.}\)
We leave it to the reader to add the commands that compute
in Assignments/Week2/C/Gemm_4x4Kernel.c. Upon completion of the loop, the results are stored back into the original arrays with the commands
_mm256_storeu_pd( &gamma(0,0), gamma_0123_0 ); _mm256_storeu_pd( &gamma(0,1), gamma_0123_1 ); _mm256_storeu_pd( &gamma(0,2), gamma_0123_2 ); _mm256_storeu_pd( &gamma(0,3), gamma_0123_3 );
Homework 2.4.3.1.
Complete the code in Assignments/Week2/C/Gemm_4x4Kernel.c and execute it with
make JI_4x4KernelView its performance with
Assignments/Week2/C/data/Plot_register_blocking.mlx
Assignments/Week2/Answers/Gemm_4x4Kernel.c
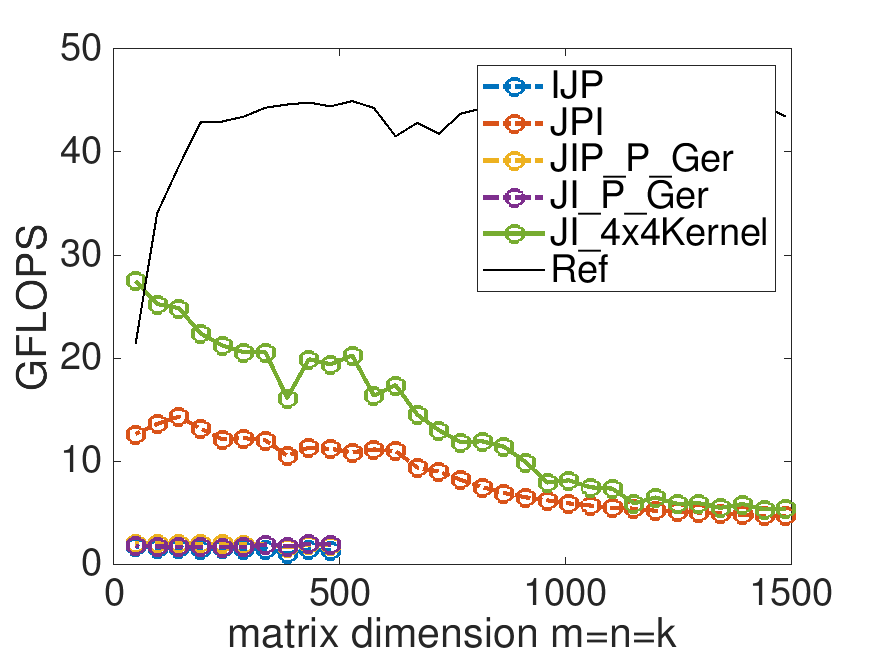
This is the performance on Robert's laptop, with MB=NB=KB=4:
Remark 2.4.5.
The form of parallelism illustrated here is often referred to as Single Instruction, Multiple Data (SIMD) parallelism since the same operation (an FMA) is executed with multiple data (four values of \(C \) and \(A \) and a duplicated value from \(B\)).
We are starting to see some progress towards higher performance