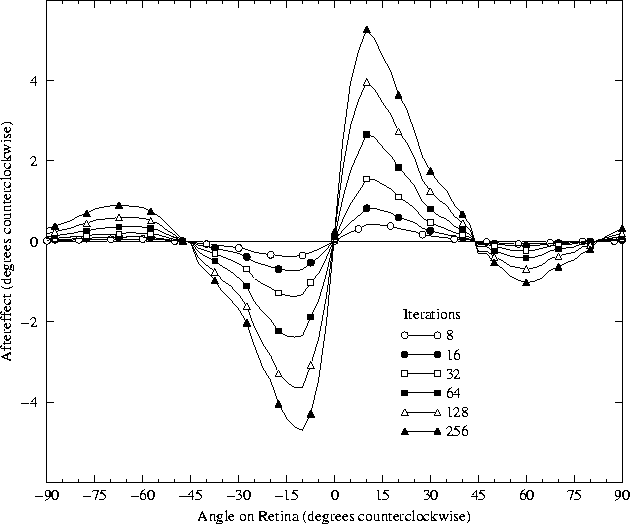
The circles show the magnitude of the TAE as a function of
adaptation time for human subjects MWG (unfilled circles) and SM
(filled circles) from
Greenlee and Magnussen (1987); they were the
only subjects tested in the study. Each subject adapted to a
single +12° line for the time period indicated on the
horizontal axis (bottom). To estimate the magnitude of the
aftereffect at each point, a vertical test line was presented at
the same location and the subject was requested to set it a
comparison line at another location to match it. The vertical
location of each point represents the average of five settings;
the data for 0 - 10 minutes were collected separately from the
rest.
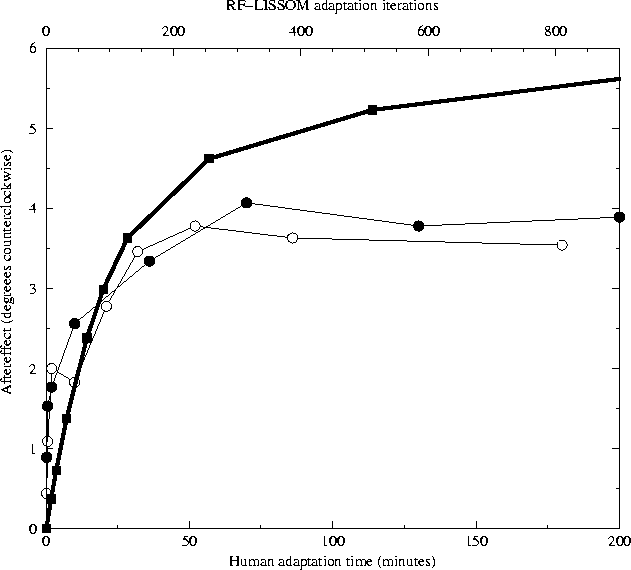
For comparison, the heavy line shows average TAE in the LISSOM
model for a +12° test line over 9 trials (with parameters as in
figure
5.2). The horizontal axis (top)
represents the number of iterations of adaptation, and the
vertical axis represents the magnitude of the TAE at this time
step.
The RF-LISSOM results show a similar logarithmic increase in TAE
magnitude with time, but do not show the saturation that is seen
for the human subjects.