 |
The TAE testing procedure described in the previous section was used to determine the amount of aftereffect for each difference between adaptation and testing orientations in the model. Figure 5.2 plots the aftereffects after adaptation for 90 iterations of the RF-LISSOM algorithm. For comparison, figure 5.2 also shows the most detailed data available for the TAE in human foveal vision (Mitchell and Muir, 1976).
 |
The results from the RF-LISSOM simulation are strikingly similar to the psychophysical results. For the range 5° to 40°, all subjects in the human study (including the one shown) exhibited angle repulsion effects nearly identical to those found in the RF-LISSOM model. The magnitude of the TAE increases very rapidly to a maximum angle repulsion at approximately 10°, falling off somewhat more gradually to zero as the angular separation increases. Section 5.4.2 examines the mechanisms responsible for these direct effects in RF-LISSOM.
The results for larger angular separations (from 45° to 85°) show a greater inter-subject variability in the psychophysical literature, but those found for the RF-LISSOM model are well within the range seen for human subjects. The indirect effects for the subject shown were typical for that study, although some subjects showed effects up to 2.5°. Section 5.4.3 examines the mechanisms responsible for these indirect effects in the RF-LISSOM model, and section 6.2.4 of the discussion proposes explanations for the variety of effects seen in human subjects.
The TAE seen in figure 5.2 must result from changes in the connection strengths between neurons, since there is no other component of the model which changes as adaptation progresses. In particular, there is no lasting change in the neuron's inherent excitability or sustained activation level. Thus there is nothing that could correspond to the concept of whole-cell neural fatigue.
Three sets of weights adapt synergetically: the afferent weights, the
lateral excitatory weights, and the lateral inhibitory weights. The
lateral inhibitory theory would predict that the inhibitory weights
are primarily responsible for the TAE magnitude at each angle. To
determine whether this is the case, the contribution of each of the
weight types was evaluated independently of the others
(figure 5.3).
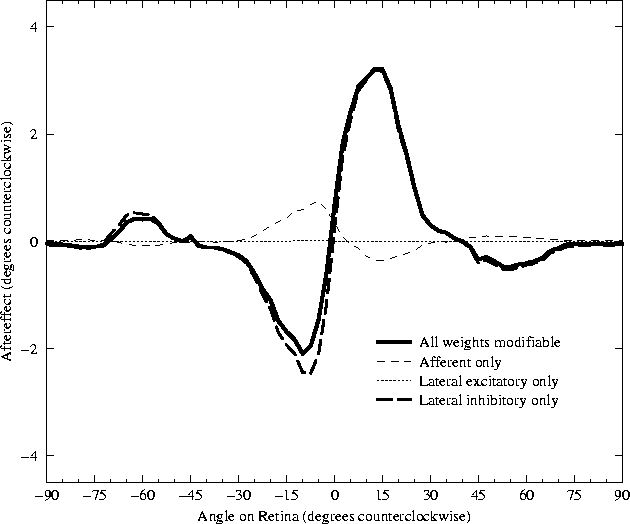 |
While the excitatory connections are adapting, the inhibitory
connections adapt as well. Each inhibitory connection adapts with the
same learning rate as the excitatory connections
(![]() ), but there are many more
inhibitory connections than excitatory connections. The combined
strength of all the small inhibitory changes outweighs the excitatory
changes, and results in a curve with a sign opposite that of the
components from the excitatory weights. If excitatory learning is
turned off altogether, the magnitude of the TAE increases slightly on
average, but the shape of the curve does not change significantly
(figure 5.3). Similar results should
be obtained if there are not as many inhibitory connections as used
here, but the ones present change more rapidly than afferent
connections; this would represent an alternative interpretation of
the results.
), but there are many more
inhibitory connections than excitatory connections. The combined
strength of all the small inhibitory changes outweighs the excitatory
changes, and results in a curve with a sign opposite that of the
components from the excitatory weights. If excitatory learning is
turned off altogether, the magnitude of the TAE increases slightly on
average, but the shape of the curve does not change significantly
(figure 5.3). Similar results should
be obtained if there are not as many inhibitory connections as used
here, but the ones present change more rapidly than afferent
connections; this would represent an alternative interpretation of
the results.
Thus the inhibitory connections are clearly responsible for both the direct and indirect tilt aftereffects observed in the RF-LISSOM model. The following sections will examine exactly how changing the inhibitory weight strength produces the effects seen. To make the analysis clear and unambiguous, the simplest case that shows a realistic TAE was chosen. The discussion will center upon a single trial, using a Gaussian at the exact center of the retina, with only the inhibitory weights adapting. The TAE curve for that case is shown in figure 5.3. The curve is still quite similar to the average result when all weights were adapting at the same rate, as well as to the human data (figure 5.2). The analysis will show that Hebbian modification of the lateral inhibitory connection weights, followed by normalization of the total connection strength, systematically alters the response in a way that results in the tilt aftereffect.