


Next: Influence of the
Up: Recurrent Inhibition and Clustered
Previous: The resultant receptive
In this section we want to analyze, in quantitative form, how the
resultant RF depends on the presence and the values of various
architectural primitives. Specifically we investigate the influence of the
orientation map and of the inhibitory schema.
The order of magnitude specification of the parameters characterizing the
model, can be guided by physiological findings:
- -
- Considering that inhibition spans over a small portion of the cortical
surface the topographic mapping is approximated with a constant, i.e.,
 , as it occurs for RF centers located between
, as it occurs for RF centers located between  and
and
 degrees from the fovea
[2].
degrees from the fovea
[2].
- -
- The dimension of the RFs is chosen taking into account the
relationships between orientation columns, field size and magnification factor.
Specifically, we fix the size of the initial RF
(
 ) in order that the average diameter of the resulting RF is
approximately twice the average wavelength (
) in order that the average diameter of the resulting RF is
approximately twice the average wavelength ( ) of the orientation
map. This ensures that the RFs of cells separated by a distance of
) of the orientation
map. This ensures that the RFs of cells separated by a distance of
 do not overlap, as reported by numerous experimental
observations
[2,58,60,61,107].
do not overlap, as reported by numerous experimental
observations
[2,58,60,61,107]. - -
- Concerning the inhibitory kernel, we set the width of each
Gaussian at
 and their relative displacement at
and their relative displacement at
 , while the excitatory gain a is kept at
, while the excitatory gain a is kept at  [64,65,67,123,125].
[64,65,67,123,125].
Typical results obtained by numerical evaluation of
(20) and (21) are shown in figure 4.
They refer to the cells marked on the orientation map depicted in
figure 3.
The effects of the increasing strength of inhibition
b on the equivalent feed-forward kernels  are shown
in the insets.
are shown
in the insets.
Figure 3: (click on the image to view a larger version)
An example of a biologically-realistic orientation map obtained according
the model proposed by (Wörgötter and Niebur, 1993). The square-areas correspond to the portion of the cortical plane which we
considered for simulations; (a) and (b) represent iso-orientation domains,
whereas (c) and (d) evidence a pinwheel and a fracture, respectively.
The marked line in the centers of the square-areas stand for
the target cell.
Figure 4:
(click on the image to view a larger version)
The resulting 2-D RF profiles, together with their contour levels, for the
target cells marked in the corresponding portions of the orientation map in
figure 3.
The results have been obtained for  (a and b) and
(a and b) and  (c and d),
respectively.
The insets show the behavior of the equivalent feed-forward kernels is shown,
for different values of the inhibition strength b (
(c and d),
respectively.
The insets show the behavior of the equivalent feed-forward kernels is shown,
for different values of the inhibition strength b ( to
to  , by
step of
, by
step of  ).
).
For low values of b, in addition to the dominant central subregion,
supplied by LGN projections, we observed in the resulting RF the presence
of parallel inhibitory flanks, which prevent responses to non-preferred
orientations. Increasing the strength of inhibition, additional sidebands
appear in the RF, endowing it with a well-defined multipartite structure
that resembles that of real ``periodic'' simple cells
[29,88,120].
The clustered nature of the modeled inhibition manages, indeed, to
establish spatial periodic induced couplings with surrounding cells that are
alternately positive and negative.
Specifically, positive couplings take place between cells with overlapping
inhibitory fields. Such induced excitatory fields contribute,
in turn, to the formation of additional negative or positive couplings with
other cells, depending on the signs of their overlapping interaction
fields. Thus, recurrent inhibition results in
an increasing extension of effective coupling over cortical plane as it
appears well evidenced in the shape of the equivalent feed-forward kernel
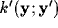 (see figure 4).
(see figure 4).



Next: Influence of the
Up: Recurrent Inhibition and Clustered
Previous: The resultant receptive
 , as it occurs for RF centers located between
, as it occurs for RF centers located between  and
and
 degrees from the fovea
[2].
degrees from the fovea
[2].
 ) in order that the average diameter of the resulting RF is
approximately twice the average wavelength (
) in order that the average diameter of the resulting RF is
approximately twice the average wavelength ( ) of the orientation
map. This ensures that the RFs of cells separated by a distance of
) of the orientation
map. This ensures that the RFs of cells separated by a distance of
 do not overlap, as reported by numerous experimental
observations
[2,58,60,61,107].
do not overlap, as reported by numerous experimental
observations
[2,58,60,61,107].  and their relative displacement at
and their relative displacement at
 , while the excitatory gain a is kept at
, while the excitatory gain a is kept at  [64,65,67,123,125].
[64,65,67,123,125].



 are shown
in the insets.
are shown
in the insets.





 (a and b) and
(a and b) and  (c and d),
respectively.
The insets show the behavior of the equivalent feed-forward kernels is shown,
for different values of the inhibition strength b (
(c and d),
respectively.
The insets show the behavior of the equivalent feed-forward kernels is shown,
for different values of the inhibition strength b ( to
to  , by
step of
, by
step of  ).
).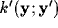 (see figure
(see figure