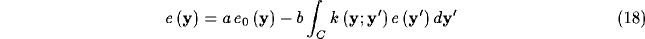



From (10), the distribution of excitation on the cortical plane can be explicitly rewritten as
where, see equations (9) and (11)
According to the method of Fredholm for inhomogeneous integral equations [121] an approximate solution of equation (18) can be expressed in the form

where


Substituting  from (19)
and
comparing the result with (8) we identify the kernel
and thence the resulting RF
from (19)
and
comparing the result with (8) we identify the kernel
and thence the resulting RF  after
recurrent inhibition:
after
recurrent inhibition:

Making explicit the parametric mapping between cortical plane (C) and visual field (S), the resulting RF can be formulated as
where
is the equivalent inhibitory kernel in the feed-forward form.
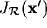 denotes the Jacobian
of
denotes the Jacobian
of  and the absolute value of its determinant is the local
magnification factor
and the absolute value of its determinant is the local
magnification factor 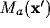 of the mapping
of the mapping  .
A more detailed derivation of this solution can be found in the Appendix.
.
A more detailed derivation of this solution can be found in the Appendix.


