Subsection 2.3.5 SVD of nonsingular matrices
¶Homework 2.3.5.1.
Let \(A \in \Cmxm \) and \(A = U \Sigma V^H \) be its SVD.
TRUE/FALSE: \(A \) is nonsingular if and only if \(\Sigma \) is nonsingular.
Homework 2.3.5.2.
Let \(A \in \Cmxm \) and \(A = U \Sigma V^H \) be its SVD with
TRUE/FALSE: \(A \) is nonsingular if and only if \(\sigma_{m-1} \neq 0 \text{.}\)
TRUE
By the last homework, \(A \) is nonsingular if and only if \(\Sigma \) is nonsingular. A diagonal matrix is nonsingular if and only if its diagonal elements are all nonzero. \(\sigma_{0} \geq \cdots \geq \sigma_{m-1} \gt 0 \text{.}\) Hence the diagonal elements of \(\Sigma \) are nonzero if and only if \(\sigma_{m-1} \neq 0 \text{.}\)
Homework 2.3.5.3.
Let \(A \in \Cmxm \) be nonsingular and \(A = U \Sigma V^H \) be its SVD.
ALWAYS/SOMETIMES/NEVER: The SVD of \(A^{-1} \) equals \(V \Sigma^{-1} U^H \text{.}\)
SOMETIMES
Explain it!
It would seem that the answer is ALWAYS: \(A^{-1} = ( U \Sigma V^H )^{-1} = (V^H)^{-1} \Sigma^{-1} U^{-1} = V \Sigma^{-1} U^H \) with
However, the SVD requires the diagonal elements to be positive and ordered from largest to smallest.
So, only if \(\sigma_0 = \sigma_1 = \cdots = \sigma_{m-1}\) is it the case that \(V \Sigma^{-1} U^H \) is the SVD of \(A^{-1} \text{.}\) In other words, when \(\Sigma = \sigma_0 I \text{.}\)
Homework 2.3.5.4.
Let \(A \in \Cmxm \) be nonsingular and
be its SVD.
The SVD of \(A^{-1} \) is given by (indicate all correct answers):
- \(V \Sigma^{-1} U^H \text{.}\)
- \(\displaystyle \left( \begin{array}{c | c | c } v_0 \amp \cdots \amp v_{m-1} \end{array} \right) \left( \begin{array}{c | c | c} 1/\sigma_{0} \amp \cdots \amp 0 \\ \hline \vdots \amp \ddots \amp \vdots \\ \hline 0 \amp \cdots \amp 1/\sigma_{m-1} \end{array} \right) \left( \begin{array}{c | c | c } u_0 \amp \cdots \amp u_{m-1} \end{array} \right)^H \)
- \(\displaystyle \left( \begin{array}{c | c | c } v_{m-1} \amp \cdots \amp v_{0} \end{array} \right) \left( \begin{array}{c | c | c} 1/\sigma_{m-1} \amp \cdots \amp 0 \\ \hline \vdots \amp \ddots \amp \vdots \\ \hline 0 \amp \cdots \amp 1/\sigma_{0} \end{array} \right) \left( \begin{array}{c | c| c } u_{m-1} \amp \cdots \amp u_{0} \end{array} \right)^H .\)
\(( V P^H ) ( P \Sigma^{-1} P^H ) ( U P^H )^H \) where \(P = \left( \begin{array}{c c c c} 0 \amp \cdots \amp 0 \amp 1 \\ 0 \amp \cdots \amp 1 \amp 0 \\ \vdots \amp \amp \vdots \amp \vdots \\ 1 \amp \cdots \amp 0 \amp 0 \end{array} \right) \)
3. and 4.
Explain it!
This question is a bit tricky.
It is the case that \(A^{-1} = V \Sigma^{-1} U^H \text{.}\) However, the diagonal elements of \(\Sigma^{-1} \) are ordered from smallest to largest, and hence this is not its SVD.
This is just Answer 1. but with the columns of \(U\) and \(V \text{,}\) and the elements of \(\Sigma \text{,}\) exposed.
This answer corrects the problems with the previous two answers: it reorders colums of \(U \) and \(V \) so that the diagonal elements of \(\Sigma\) end up ordered from largest to smallest.
This answer is just a reformulation of the last answer.
Homework 2.3.5.5.
Let \(A \in \Cmxm \) be nonsingular.
TRUE/FALSE: \(\| A^{-1} \|_2 = 1 / \min_{\| x \|_2 = 1} \| A x \|_2 \text{.}\)
TRUE
In Subsection 2.3.2, we discussed the case where \(A \in \R^{2 \times 2} \text{.}\) Letting \(A = U \Sigma V^T \) and partitioning
yielded the pictures
\(\R^{2} \text{:}\) Domain of \(A \text{:}\)
\(\R^{2} \text{:}\) Range (codomain) of \(A \text{:}\)
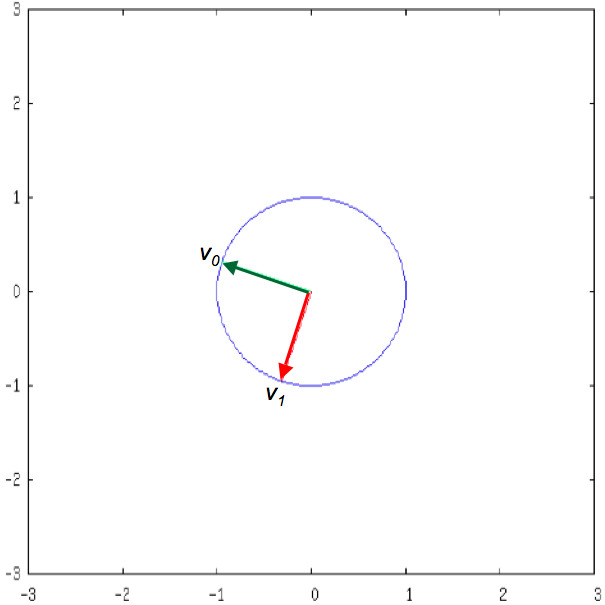
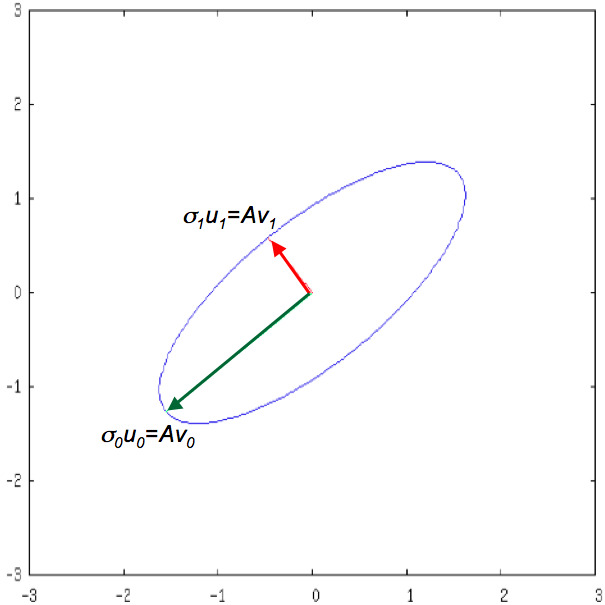
This captures what the condition number \(\kappa_2( A ) = \sigma_0 / \sigma_{n-1} \) captures: how elongated the oval that equals the image of the unit ball is. The more elongated, the greater the ratio \(\sigma_0 / \sigma_{n-1} \text{,}\) and the worse the condition number of the matrix. In the limit, when \(\sigma_{n-1} = 0 \text{,}\) the unit ball is mapped to a lower dimensional set, meaning that the transformation cannot be "undone."
Ponder This 2.3.5.6.
For the 2D problem discussed in this unit, what would the image of the unit ball look like as \(\kappa_2( A ) \rightarrow \infty \text{?}\) When is \(\kappa_2( A ) = \infty \text{?}\)
